|
| 1 | +3219\. Minimum Cost for Cutting Cake II |
| 2 | + |
| 3 | +Hard |
| 4 | + |
| 5 | +There is an `m x n` cake that needs to be cut into `1 x 1` pieces. |
| 6 | + |
| 7 | +You are given integers `m`, `n`, and two arrays: |
| 8 | + |
| 9 | +* `horizontalCut` of size `m - 1`, where `horizontalCut[i]` represents the cost to cut along the horizontal line `i`. |
| 10 | +* `verticalCut` of size `n - 1`, where `verticalCut[j]` represents the cost to cut along the vertical line `j`. |
| 11 | + |
| 12 | +In one operation, you can choose any piece of cake that is not yet a `1 x 1` square and perform one of the following cuts: |
| 13 | + |
| 14 | +1. Cut along a horizontal line `i` at a cost of `horizontalCut[i]`. |
| 15 | +2. Cut along a vertical line `j` at a cost of `verticalCut[j]`. |
| 16 | + |
| 17 | +After the cut, the piece of cake is divided into two distinct pieces. |
| 18 | + |
| 19 | +The cost of a cut depends only on the initial cost of the line and does not change. |
| 20 | + |
| 21 | +Return the **minimum** total cost to cut the entire cake into `1 x 1` pieces. |
| 22 | + |
| 23 | +**Example 1:** |
| 24 | + |
| 25 | +**Input:** m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5] |
| 26 | + |
| 27 | +**Output:** 13 |
| 28 | + |
| 29 | +**Explanation:** |
| 30 | + |
| 31 | +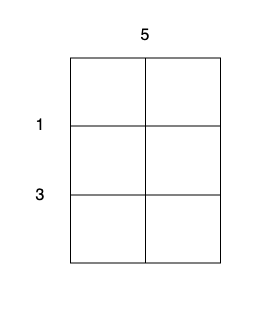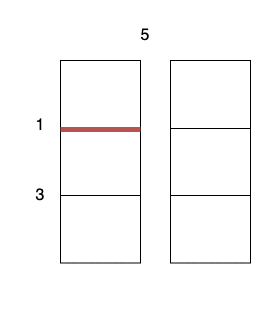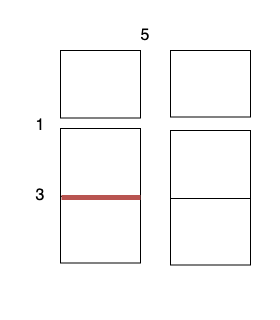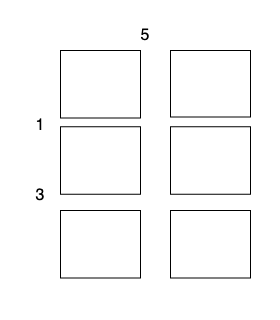 |
| 32 | + |
| 33 | +* Perform a cut on the vertical line 0 with cost 5, current total cost is 5. |
| 34 | +* Perform a cut on the horizontal line 0 on `3 x 1` subgrid with cost 1. |
| 35 | +* Perform a cut on the horizontal line 0 on `3 x 1` subgrid with cost 1. |
| 36 | +* Perform a cut on the horizontal line 1 on `2 x 1` subgrid with cost 3. |
| 37 | +* Perform a cut on the horizontal line 1 on `2 x 1` subgrid with cost 3. |
| 38 | + |
| 39 | +The total cost is `5 + 1 + 1 + 3 + 3 = 13`. |
| 40 | + |
| 41 | +**Example 2:** |
| 42 | + |
| 43 | +**Input:** m = 2, n = 2, horizontalCut = [7], verticalCut = [4] |
| 44 | + |
| 45 | +**Output:** 15 |
| 46 | + |
| 47 | +**Explanation:** |
| 48 | + |
| 49 | +* Perform a cut on the horizontal line 0 with cost 7. |
| 50 | +* Perform a cut on the vertical line 0 on `1 x 2` subgrid with cost 4. |
| 51 | +* Perform a cut on the vertical line 0 on `1 x 2` subgrid with cost 4. |
| 52 | + |
| 53 | +The total cost is `7 + 4 + 4 = 15`. |
| 54 | + |
| 55 | +**Constraints:** |
| 56 | + |
| 57 | +* <code>1 <= m, n <= 10<sup>5</sup></code> |
| 58 | +* `horizontalCut.length == m - 1` |
| 59 | +* `verticalCut.length == n - 1` |
| 60 | +* <code>1 <= horizontalCut[i], verticalCut[i] <= 10<sup>3</sup></code> |
0 commit comments