Update continued-fractions.md

Oleksandr Kulkov · web-flow · commit e6c5c73a3258 · 2021-12-21T14:18:33.000+01:00
expansion
diff --git a/src/algebra/continued-fractions.md b/src/algebra/continued-fractions.md
@@ -142,24 +142,24 @@ On the other hand, $a_k$ may be defined as $a_k = \lfloor s_k \rfloor$, thus we
 
 ## Convergence
 
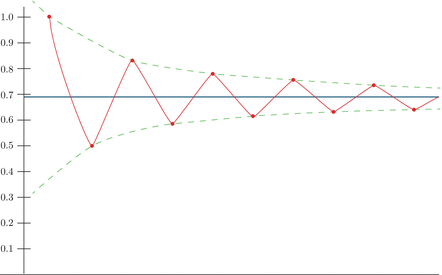
-Now that we have some explicit formulas for convergent numbers, let's estimate their distance to the final number $r$. First of all, we can estimate the difference between adjacent convergents:
+Let's estimate the distance between $r_k$ and the limit number $r$. The difference between adjacent convergents is given as
 
-$$\frac{p_k}{q_k} - \frac{p_{k-1}}{q_{k-1}} = \frac{p_k q_{k-1} - p_{k-1} q_k}{q_k q_{k-1}}$$
+$$\frac{p_k}{q_k} - \frac{p_{k-1}}{q_{k-1}} = \frac{p_k q_{k-1} - p_{k-1} q_k}{q_k q_{k-1}}.$$
 
-For the numerator of this fraction, it is possible to get rid of numbers with index $k$:
+If $p_k$ and $q_k$ in the numerator are replaced with their corresponding recurrences, we get
 
 $$\begin{align} p_k q_{k-1} - p_{k-1} q_k &= (a_k p_{k-1} + p_{k-2}) q_{k-1} - p_{k-1} (a_k q_{k-1} + q_{k-2})
-\\&= p_{k-2} q_{k-1} - p_{k-1} q_{k-2}\end{align}$$
+\\&= p_{k-2} q_{k-1} - p_{k-1} q_{k-2},\end{align}$$
 
-Thus, the numerator of $r_k - r_{k-1}$ is always the opposite to the numerator of $r_{k-1} - r_{k-2}$. It is equal to $1$ for $a_1 - a_0$, therefore
+Which means that the numerator of $r_k - r_{k-1}$ is always the negated numerator of $r_{k-1} - r_{k-2}$. It's equal to $1$ for $a_1 - a_0$, thus
 
-$$r_k - r_{k-1} = \frac{(-1)^{k-1}}{q_k q_{k-1}}$$
+$$r_k - r_{k-1} = \frac{(-1)^{k-1}}{q_k q_{k-1}}.$$
 
 
-This allows for alternative representation of $r_k$ as a partial sum of infinite series:
+This yields the alternative representation of $r_k$ as a partial sum of infinite series:
 
 $$r_k = (r_k - r_{k-1}) + \dots + (r_1 - r_0) + r_0
-= a_0 + \sum\limits_{i=1}^k \frac{(-1)^{i-1}}{q_i q_{i-1}}$$
+= a_0 + \sum\limits_{i=1}^k \frac{(-1)^{i-1}}{q_i q_{i-1}}.$$
 
 By definition, $q_k$ monotonically increases at least as fast as Fibonacci numbers, thus
 
@@ -169,12 +169,57 @@ is always well-defined. Noteworthy, the residual series
 
 $$r-r_k = \sum\limits_{i=k+1}^\infty \frac{(-1)^{i-1}}{q_i q_{i-1}}$$
 
-always has the same sign as $(-1)^k$ due to how fast $q_i q_{i-1}$ decreases. It means that even-indexed $r_k$ monotonously approach $r$ from below while odd-indexed $r_k$ monotonously approach it from above:
+has the same sign as $(-1)^k$ due to how fast $q_i q_{i-1}$ decreases. It means that even-indexed $r_k$ monotonously approach $r$ from below while odd-indexed $r_k$ monotonously approach it from above:
 
 <center>
 ![Convergence towards underlying number](https://codeforces.com/predownloaded/ca/8d/ca8d8835864ccccea90e458e3d8fa840a6143c13.gif)
 </center>
 
 From this picture we can see that, in fact, distance between $r$ and $r_k$ is never larger than the distance between $r_k$ and $r_{k+1}$, therefore
 
-$$\left|r-\frac{p_k}{q_k}\right| \leq \frac{1}{q_k q_{k+1}} \leq \frac{1}{q_k^2}$$
+$$\left|r-\frac{p_k}{q_k}\right| \leq \frac{1}{q_k q_{k+1}} \leq \frac{1}{q_k^2}.$$
+
+## Geometric interpretation
+
+If convergents $r_0, r_1, \dots$ are treated as 2-dimensional vectors $\vec r_k=(q_k;p_k)$, the mediant formula above turns into
+
+$$\vec r_k = a_k \vec r_{k-1} + \vec r_{k-2}.$$
+
+To better understand geometric meaning of $\vec r_k$ we need to look closer into computation of $a_k$. Previously we investigated _convergents_ $r_k = [a_0, a_1, \dots, a_k]$. Let's now look on _residuals_ $s_k = [a_{k}, a_{k+1}, \dots]$. From their definition it holds that
+
+$$s_k = a_{k} + \frac{1}{s_{k+1}}.$$
+
+Starting with $s_0=r$, it is possible to derive similar recurrent formulas for $s_k=\frac{b_k}{c_k}$:
+
+$$\frac{b_k}{c_k}=a_k + \frac{c_{k+1}}{b_{k+1}}.$$
+
+Thus, $b_{k+1}=c_k$ and $c_{k+1} = b_k - c_k a_k = c_{k-1} - c_k a_k$. This expression looks very similar to the recurrence for $p_k$ and from the starting points $s_0=\frac{r}{1}$ and $s_1 = \frac{1}{r-a_0}$ we may derive the explicit continuant formula for $c_k$:
+
+$$c_k = P_{k-1}(r-a_0, -a_1, \dots, -a_{k-1}).$$
+
+Taking into consideration the continuant properties (which follow from its determinant definition)
+
+$$\begin{align}
+P_k(a_0, \dots, a_k) &= (-1)^{k+1} P_k(-a_0, \dots, -a_k),\\
+P_k(a_0, \dots, a_k) &= a_0 P_{k-1}(a_1, \dots, a_k) + P_{k-2}(a_2, \dots, a_k),
+\end{align}$$
+
+we may rearrange the expression for $c_k$ in a much simpler manner:
+
+$$c_k = (-1)^{k-1} (r q_{k-1} - p_{k-1}).$$
+
+This gives us the final formula to calculate residual $s_k$ from convergents:
+
+$$s_k = \left|\frac{rq_{k-2} - p_{k-2}}{rq_{k-1} - p_{k-1}}\right| = \frac{q_{k-2}}{q_{k-1}}\left|\frac{r - r_{k-2}}{r - r_{k-1}}\right|.$$
+
+On the other hand, $a_k$ may be defined as $a_k = \lfloor s_k \rfloor$, thus we have more explicit expression for $a_k$ as well. But what is its geometric meaning in terms of $\vec r_{k-1}$ and $\vec r_{k-2}$?
+
+### Nose stretching
+
+From convergence section we know that the number $r$ always lies between numbers $r_{k-1}$ and $r_{k-2}$. For $\vec r_{k-1}$ and $\vec r_{k-2}$ it means that they are always on the opposite sides of the vector $\vec r = (1;r)$. This is due to $r_{k-1}=\frac{p_{k-1}}{q_{k-1}}$ and $r_{k-2}=\frac{p_{k-2}}{q_{k-2}}$ being slope coefficients of $\vec r_{k-1}$ and $\vec r_{k-2}$ correspondingly, while slope coefficient of $\vec r$ is exactly $r$.
+
+Geometrically, $r q_{k-1} - p_{k-1}$ is equal to $\vec r_{k-1} \times \vec r$, that is, the cross product of $\vec r_{k-1}$ and $\vec r$. Thus, the explicit $\vec r$ formula is
+
+$$\vec r = \vec r_{k-2} + \left \lfloor \left|\frac{\vec r_{k-2} \times \vec r}{\vec r_{k-1} \times \vec r} \right|\right \rfloor \cdot \vec r_{k-1}.$$
+
+Geometrically, $a_k$ here is equal to the maximum integer number of $\vec r_{k-1}$ vectors that can be added to $\vec r_{k-2}$ in such a way that the resulting vector will still be on the same side from $\vec r$ as $\vec r_{k-2}$ is.
