3D rendering is really easy once you've understood a few concepts. To demonstrate that, we'll design a simple custom 3D engine that with 60 lines of Python and one Matplotlib call. That is, we'll render the bunny without using the 3D axis.
Posted
#tutorials #3D
UNC BIOL222: Art created with Matplotlib
Posted
#art #academia
Many figures in the IPCC SR15 were generated using Matplotlib. +The data and open-source notebooks were published to increase the transparency and reproducibility of the analysis.
Posted
#academia #tutorials
Ed Hawkins made this impressively simple plot to show how global temperatures have risen since 1880. Here is how to recreate it using Matplotlib.
Posted
#tutorials #academia
Advocating is all about communicating facts clearly. I used Matplotlib to show the financial struggles of postdocs in the Boston area.
Posted
#academia
UNC BIOL222: Art created with Matplotlib
Posted
#art #academia
Applied image manipulation to create procedural art.
Posted
#tutorials #art
Matplotblog, the new blog of Matplotlib, to showcase and share great visualization stories.
Posted
#editorial
The Python Graph Gallery is a website that displays hundreds of chart examples made with python. It goes from very basic to highly customized examples and is based on common viz libraries like matplotlib, seaborn or plotly.
Posted
#tutorials #graphs
Learn how to easily create step charts through examining the multilingualism of pop group WayV
Posted
#tutorials #graphs
A fun project about drawing all possible differently-looking (not isomorphic) graphs of N nodes.
Posted
#tutorials #graphs
Google Summer of Code 2021: Final Report - Aitik Gupta
Posted
#News #GSoC
Quarter Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
Pre-Quarter Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
Mid-Term Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
Introduction about Aitik Gupta, Google Summer of Code 2021 Intern under the parent organisation: NumFOCUS
Posted
#News #GSoC
Final Work Product Report for the Google Summer of Code 2020 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the first half of the Google Summer of Code 2020 Phase 3 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the second half of the Google Summer of Code 2020 Phase 2 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the first half of the Google Summer of Code 2020 Phase 2 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the second half of the Google Summer of Code 2020 Phase 1 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the first half of the Google Summer of Code 2020 Phase 1 for the Baseline Images Problem
Posted
#News #GSoC
Introductory post about Sidharth Bansal, Google Summer of Code 2020 Intern for Baseline Image Problem Project under Numfocus
Posted
#News #GSoC
This is my first post contribution to Matplotlib.
Posted
#GSoD
Posted
Posted
Posted
Posted
At Whites Agency we analyze big unstructured data to increases client's online visibility. We share our story of how we used Matplotlib to present the complicated data in a simple and reader-friendly way.
Posted
#industry
New open access book released
Posted
#News
Google Summer of Code 2021: Final Report - Aitik Gupta
Posted
#News #GSoC
Quarter Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
Pre-Quarter Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
Mid-Term Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
Introduction about Aitik Gupta, Google Summer of Code 2021 Intern under the parent organisation: NumFOCUS
Posted
#News #GSoC
Final Work Product Report for the Google Summer of Code 2020 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the first half of the Google Summer of Code 2020 Phase 3 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the second half of the Google Summer of Code 2020 Phase 2 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the first half of the Google Summer of Code 2020 Phase 2 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the second half of the Google Summer of Code 2020 Phase 1 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the first half of the Google Summer of Code 2020 Phase 1 for the Baseline Images Problem
Posted
#News #GSoC
Introductory post about Sidharth Bansal, Google Summer of Code 2020 Intern for Baseline Image Problem Project under Numfocus
Posted
#News #GSoC
We have hired Elliott Sales de Andrade as the Matplotlib Software Research Engineering Fellow supported by the Chan Zuckerberg Initiative Essential Open Source Software for Science
Posted
#News
Posted
Posted
Posted
Posted
Posted
Posted
A tutorial on how to create custom tables in Matplotlib which allow for flexible design and customization.
Posted
#tutorials
A tutorial on how to show usage rates and more using batteries
Posted
#tutorials
The Python Graph Gallery is a website that displays hundreds of chart examples made with python. It goes from very basic to highly customized examples and is based on common viz libraries like matplotlib, seaborn or plotly.
Posted
#tutorials #graphs
Learn how to create a simple stellar chart, an alternative to the radar chart.
Posted
#tutorials
Many figures in the IPCC SR15 were generated using Matplotlib. +The data and open-source notebooks were published to increase the transparency and reproducibility of the analysis.
Posted
#academia #tutorials
Learn how to easily create step charts through examining the multilingualism of pop group WayV
Posted
#tutorials #graphs
A brief tour through the world of elementary cellular automata
Posted
#tutorials
Discover the bizarre geometry of the fractals and learn how to make an animated visualization of these marvels using Python and the Matplotlib's Animation API.
Posted
#tutorials
This post describes how to animate some oceanographic measurements in a tweaked polar plot
Posted
#tutorials
Applied image manipulation to create procedural art.
Posted
#tutorials #art
A fun project about drawing all possible differently-looking (not isomorphic) graphs of N nodes.
Posted
#tutorials #graphs
Futuristic neon glow for your next data visualization
Posted
#tutorials
How to use Matplotlib to make diagrams.
Posted
#tutorials
This post details how to leverage gridspec to create ridgeplots in Matplotlib
Posted
#tutorials
Learn how to create a Tesla Cybertruck with Matplotlib that drives via animation.
Posted
#tutorials
This guide dives deep into the inner workings of Matplotlib's Figures, Axes, subplots and the very amazing GridSpec!
Posted
#tutorials
3D rendering is really easy once you've understood a few concepts. To demonstrate that, we'll design a simple custom 3D engine that with 60 lines of Python and one Matplotlib call. That is, we'll render the bunny without using the 3D axis.
Posted
#tutorials #3D
Ed Hawkins made this impressively simple plot to show how global temperatures have risen since 1880. Here is how to recreate it using Matplotlib.
Posted
#tutorials #academia
See how you can contribute to the matplotblog.
Posted
#tutorials
- Previous (notice Tofus) VS After (CJK font as fallback) -
- -To migrate from a font-first approach to a text-first approach, there are multiple steps involved: - -### Parsing the whole font family -The very first (and crucial!) step is to get to a point where we have multiple font paths (ideally individual font files for the whole family). That is achieved with either: -- [PR: [with findfont diff] Parsing all families in font_manager](https://github.com/matplotlib/matplotlib/pull/20496), or -- [PR: [without findfont diff] Parsing all families in font_manager](https://github.com/matplotlib/matplotlib/pull/20549) - -Quoting one of my [previous](https://matplotlib.org/matplotblog/posts/gsoc_2021_prequarter/) blogs: -> Don’t break, a lot at stake! - -My first approach was to change the existing public `findfont` API to incorporate multiple filepaths. Since Matplotlib has a _very huge_ userbase, there's a high chance it would break a chunk of people's workflow: - -
- 
- First PR (left), Second PR (right)
-
- 
- Font-Fallback Algorithm
-
- 
- Consider contributing to Matplotlib (Open Source in general) ❤️
-
-
-
-## Getting started with Matplotlib
-It was around initial weeks of November last year, I was scanning through `Good First Issue` and `New Feature` labels, I realised a pattern - most Mathtext related issues were unattended.
-
-To make it simple, Mathtext is a part of Matplotlib which parses mathematical expressions and provides TeX-like outputs, for example:
-
-
-I scanned the related source code to try to figure out how to solve those Mathtext issues. Eventually, with the help of maintainers reviewing the PRs and a lot of verbose discussions on GitHub issues/pull requests and on the [Gitter](https://gitter.im/matplotlib/matplotlib) channel, I was able to get my initial PRs merged!
-
-## Learning throughout the process
-Most of us use libraries without understanding the underlining structure of them, which sometimes can cause downstream bugs!
-
-While I was studying Matplotlib's architecture, I figured that I could use the same ideology for one of my [own projects](https://aitikgupta.github.io/swi-ml/)!
-
-Matplotlib uses a global dictionary-like object named as `rcParams`, I used a smaller interface, similar to rcParams, in [swi-ml](https://pypi.org/project/swi-ml/) - a small Python library I wrote, implementing a subset of ML algorithms, with a switchable backend.
-
-
-## Where does GSoC fit?
-It was around January, I had a conversation with one of the maintainers (hey [Antony](https://github.com/anntzer)!) about the long-list of issues with the current ways of handling texts/fonts in the library.
-
-After compiling them into an order, after few tweaks from maintainers, [GSoC Idea-List](https://github.com/matplotlib/matplotlib/wiki/GSOC-2021-ideas) for Matplotlib was born. And so did my journey of building a strong proposal!
-
-## About the Project
-#### Proposal Link: [Google Docs](https://docs.google.com/document/d/11PrXKjMHhl0rcQB4p_W9JY_AbPCkYuoTT0t85937nB0/edit?usp=sharing) (will stay alive after GSoC), [GSoC Website](https://storage.googleapis.com/summerofcode-prod.appspot.com/gsoc/core_project/doc/6319153410998272_1617936740_GSoC_Proposal_-_Matplotlib.pdf?Expires=1621539234&GoogleAccessId=summerofcode-prod%40appspot.gserviceaccount.com&Signature=QU8uSdPnXpa%2FooDtzVnzclz809LHjh9eU7Y7iR%2FH1NM32CBgzBO4%2FFbMeDmMsoic91B%2BKrPZEljzGt%2Fx9jtQeCR9X4O53JJLPVjw9Bg%2Fzb2YKjGzDk0oFMRPXjg9ct%2BV58PD6f4De1ucqARLtHGjis5jhK1W08LNiHAo88NB6BaL8Q5hqcTBgunLytTNBJh5lW2kD8eR2WeENnW9HdIe53aCdyxJkYpkgILJRoNLCvp111AJGC3RLYba9VKeU6w2CdrumPfRP45FX6fJlrKnClvxyf5VHo3uIjA3fGNWIQKwGgcd1ocGuFN3YnDTS4xkX3uiNplwTM4aGLQNhtrMqA%3D%3D) (not so sure)
-
-### Revisiting Text/Font Handling
-The aim of the project is divided into 3 subgoals:
-
-1. **Font-Fallback**: A redesigned text-first font interface - essentially parsing all family before rendering a "tofu".
-
- *(similar to specifying font-family in CSS!)*
-2. **Font Subsetting**: Every exported PS/PDF would contain embedded glyphs subsetted from the whole font.
-
- *(imagine a plot with just a single letter "a", would you like it if the PDF you exported from Matplotlib to embed the whole font file within it?)*
-
-3. Most mpl backends would use the unified TeX exporting mechanism
-
-**Mentors** [Thomas A Caswell](https://github.com/tacaswell), [Antony Lee](https://github.com/anntzer), [Hannah](https://github.com/story645).
-
-Thanks a lot for spending time reading the blog! I'll be back with my progress in subsequent posts.
-
-
-##### NOTE: This blog post is also available at my [personal website](https://aitikgupta.github.io/gsoc-intro/)!
-
diff --git a/content/posts/GSoC_2021_MidTerm/index.md b/content/posts/GSoC_2021_MidTerm/index.md
deleted file mode 100644
index dece87c..0000000
--- a/content/posts/GSoC_2021_MidTerm/index.md
+++ /dev/null
@@ -1,88 +0,0 @@
----
-title: "GSoC'21: Mid-Term Progress"
-date: 2021-07-02T08:32:05+05:30
-draft: false
-categories: ["News", "GSoC"]
-description: "Mid-Term Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta"
-displayInList: true
-author: Aitik Gupta
-
-resources:
-- name: featuredImage
- src: "AitikGupta_GSoC.png"
- params:
- showOnTop: true
----
-
-**"Aitik, how is your GSoC going?"**
-
-Well, it's been a while since I last wrote. But I wasn't spending time watching _Loki_ either! (that's a lie.)
-
-During this period the project took on some interesting (and stressful) curves, which I intend to talk about in this small writeup.
-## New Mentor!
-The first week of coding period, and I met one of my new mentors, [Jouni](https://github.com/jkseppan). Without him, along with [Tom](https://github.com/tacaswell) and [Antony](https://github.com/anntzer), the project wouldn't have moved _an inch_.
-
-It was initially Jouni's [PR](https://github.com/matplotlib/matplotlib/pull/18143) which was my starting point of the first milestone in my proposal, Font Subsetting.
-
-## What is Font Subsetting anyway?
-As was proposed by Tom, a good way to understand something is to document your journey along the way! (well, that's what GSoC wants us to follow anyway right?)
-
-Taking an excerpt from one of the paragraphs I wrote [here](https://github.com/matplotlib/matplotlib/blob/a94f52121cea4194a5d6f6fc94eafdfb03394628/doc/users/fonts.rst#subsetting):
-> Font Subsetting can be used before generating documents, to embed only the _required_ glyphs within the documents. Fonts can be considered as a collection of these glyphs, so ultimately the goal of subsetting is to find out which glyphs are required for a certain array of characters, and embed only those within the output.
-
-Now this may seem straightforward, right?
-#### Wrong.
-The glyph programs can call their own subprograms, for example, characters like `ä` could be composed by calling subprograms for `a` and `¨`; or `→` could be composed by a program that changes the display matrix and calls the subprogram for `←`.
-
-Since the subsetter has to find out _all such subprograms_ being called by _every glyph_ included in the subset, this is a generally difficult problem!
-
-Something which one of my mentors said which _really_ stuck with me:
-> Matplotlib isn't a font library, and shouldn't try to be one.
-
-It's really easy to fall into the trap of trying to do _everything_ within your own project, which ends up rather _hurting_ itself.
-
-Since this holds true even for Matplotlib, it uses external dependencies like [FreeType](https://www.freetype.org/), [ttconv](https://github.com/sandflow/ttconv), and newly proposed [fontTools](https://github.com/fonttools/fonttools) to handle font subsetting, embedding, rendering, and related stuff.
-
-PS: If that font stuff didn't make sense, I would recommend going through a friendly tutorial I wrote, which is all about [Matplotlib and Fonts](https://matplotlib.org/stable/users/fonts.html)!
-## Unexpected Complications
-Matplotlib uses an external dependency `ttconv` which was initially forked into Matplotlib's repository **in 2003**!
-> ttconv was a standalone commandline utility for converting TrueType fonts to subsetted Type 3 fonts (among other features) written in 1995, which Matplotlib forked in order to make it work as a library.
-
-Over the time, there were a lot of issues with it which were either hard to fix, or didn't attract a lot of attention. (See the above paragraph for a valid reason)
-
-One major utility which is still used is `convert_ttf_to_ps`, which takes a _font path_ as input and converts it into a Type 3 or Type 42 PostScript font, which can be embedded within PS/EPS output documents. The guide I wrote ([link](https://matplotlib.org/stable/users/fonts.html)) contains decent descriptions, the differences between these type of fonts, etc.
-
-#### So we need to convert that _font path_ input to a _font buffer_ input.
-Why do we need to? Type 42 subsetting isn't really supported by ttconv, so we use a new dependency called fontTools, whose 'full-time job' is to subset Type 42 fonts for us (among other things).
-
-> It provides us with a font buffer, however ttconv expects a font path to embed that font
-
-Easily enough, this can be done by Python's `tempfile.NamedTemporaryFile`:
-```python
-with tempfile.NamedTemporaryFile(suffix=".ttf") as tmp:
- # fontdata is the subsetted buffer
- # returned from fontTools
- tmp.write(fontdata.getvalue())
-
- # TODO: allow convert_ttf_to_ps
- # to input file objects (BytesIO)
- convert_ttf_to_ps(
- os.fsencode(tmp.name),
- fh,
- fonttype,
- glyph_ids,
- )
-```
-
-***But this is far from a clean API; in terms of separation of \*reading\* the file from \*parsing\* the data.***
-
-What we _ideally_ want is to pass the buffer down to `convert_ttf_to_ps`, and modify the embedding code of `ttconv` (written in C++). And _here_ we come across a lot of unexplored codebase, _which wasn't touched a lot ever since it was forked_.
-
-Funnily enough, just yesterday, after spending a lot of quality time, me and my mentors figured out that the **whole logging system of ttconv was broken**, all because of a single debugging function. 🥲
-
-
- 
-
- 
-
- 
-
- 
- 
- 
diff --git a/content/posts/matplotlib-cyberpunk-style/index.md b/content/posts/matplotlib-cyberpunk-style/index.md
deleted file mode 100644
index 7445890..0000000
--- a/content/posts/matplotlib-cyberpunk-style/index.md
+++ /dev/null
@@ -1,150 +0,0 @@
----
-title: "Matplotlib Cyberpunk Style"
-date: 2020-03-27T20:26:07+01:00
-draft: false
-description: "Futuristic neon glow for your next data visualization"
-categories: ["tutorials"]
-displayInList: true
-author: Dominik Haitz
-
-resources:
-- name: featuredImage
- src: "figures/5.png"
- params:
- showOnTop: false
----
-
-
-## 1 - The Basis
-Let's make up some numbers, put them in a Pandas dataframe and plot them:
-
- import pandas as pd
- import matplotlib.pyplot as plt
-
- df = pd.DataFrame({'A': [1, 3, 9, 5, 2, 1, 1],
- 'B': [4, 5, 5, 7, 9, 8, 6]})
-
- df.plot(marker='o')
- plt.show()
-
-
-
-## 2 - The Darkness
-
-Not bad, but somewhat ordinary. Let's customize it by using Seaborn's dark style, as well as changing background and font colors:
-
- plt.style.use("seaborn-dark")
-
- for param in ['figure.facecolor', 'axes.facecolor', 'savefig.facecolor']:
- plt.rcParams[param] = '#212946' # bluish dark grey
-
- for param in ['text.color', 'axes.labelcolor', 'xtick.color', 'ytick.color']:
- plt.rcParams[param] = '0.9' # very light grey
-
- ax.grid(color='#2A3459') # bluish dark grey, but slightly lighter than background
-
-
-
-## 3 - The Light
-
-It looks more interesting now, but we need our colors to shine more against the dark background:
-
- fig, ax = plt.subplots()
- colors = [
- '#08F7FE', # teal/cyan
- '#FE53BB', # pink
- '#F5D300', # yellow
- '#00ff41', # matrix green
- ]
- df.plot(marker='o', ax=ax, color=colors)
-
-
-
-
-## 4 - The Glow
-
-Now, how to get that neon look? To make it shine, we *redraw the lines multiple times*, with low alpha value and slighty increasing linewidth. The overlap creates the glow effect.
-
-
- n_lines = 10
- diff_linewidth = 1.05
- alpha_value = 0.03
-
- for n in range(1, n_lines+1):
-
- df.plot(marker='o',
- linewidth=2+(diff_linewidth*n),
- alpha=alpha_value,
- legend=False,
- ax=ax,
- color=colors)
-
-
-
-
-## 5 - The Finish
-
-For some more fine tuning, we color the area below the line (via `ax.fill_between`) and adjust the axis limits.
-
-Here's the full code:
-
- import pandas as pd
- import matplotlib.pyplot as plt
-
-
- plt.style.use("dark_background")
-
- for param in ['text.color', 'axes.labelcolor', 'xtick.color', 'ytick.color']:
- plt.rcParams[param] = '0.9' # very light grey
-
- for param in ['figure.facecolor', 'axes.facecolor', 'savefig.facecolor']:
- plt.rcParams[param] = '#212946' # bluish dark grey
-
- colors = [
- '#08F7FE', # teal/cyan
- '#FE53BB', # pink
- '#F5D300', # yellow
- '#00ff41', # matrix green
- ]
-
-
- df = pd.DataFrame({'A': [1, 3, 9, 5, 2, 1, 1],
- 'B': [4, 5, 5, 7, 9, 8, 6]})
-
- fig, ax = plt.subplots()
-
- df.plot(marker='o', color=colors, ax=ax)
-
- # Redraw the data with low alpha and slighty increased linewidth:
- n_shades = 10
- diff_linewidth = 1.05
- alpha_value = 0.3 / n_shades
-
- for n in range(1, n_shades+1):
-
- df.plot(marker='o',
- linewidth=2+(diff_linewidth*n),
- alpha=alpha_value,
- legend=False,
- ax=ax,
- color=colors)
-
- # Color the areas below the lines:
- for column, color in zip(df, colors):
- ax.fill_between(x=df.index,
- y1=df[column].values,
- y2=[0] * len(df),
- color=color,
- alpha=0.1)
-
- ax.grid(color='#2A3459')
-
- ax.set_xlim([ax.get_xlim()[0] - 0.2, ax.get_xlim()[1] + 0.2]) # to not have the markers cut off
- ax.set_ylim(0)
-
- plt.show()
-
-
-
-
-If this helps you or if you have constructive criticism, I'd be happy to hear about it! Please contact me via [here](https://dhaitz.github.io) or [here](https://twitter.com/d_haitz). Thanks!
diff --git a/content/posts/matplotlib-in-data-driven-seo/index.md b/content/posts/matplotlib-in-data-driven-seo/index.md
deleted file mode 100644
index 0c05f87..0000000
--- a/content/posts/matplotlib-in-data-driven-seo/index.md
+++ /dev/null
@@ -1,181 +0,0 @@
----
-title: "Matplotlib in Data Driven SEO"
-date: 2019-12-04T17:23:24+01:00
-description: "At Whites Agency we analyze big unstructured data to increases client's online visibility. We share our story of how we used Matplotlib to present the complicated data in a simple and reader-friendly way."
-categories: ["industry"]
-draft: false
-displayInMenu: false
-displayInList: true
-author: Whites Agency
-
-resources:
-- name: featuredImage
- src: "featuredImage.png"
- params:
- showOnTop: false
----
-
-
-Search Engine Optimization (SEO) is a process that aims to increase quantity and quality of website traffic by ensuring a website can be found in search engines for phrases that are relevant to what the site is offering. Google is the most popular search engine in the world and presence in top search results is invaluable for any online business since click rates drop exponentially with ranking position. Since the beginning, specialized entities have been decoding signals that influence position in search engine result page (SERP) focusing on e.g. number of outlinks, presence of keywords or content length. Developed practices typically resulted in better visibility, but needed to be constantly challenged because search engines introduce changes to their algorithms even every day. Since the rapid advancements in Big Data and machine learning finding significant ranking factors became increasingly more difficult. Thus, the whole SEO field required a shift where recommendations are backed up by large scale studies based on real data rather than old-fashioned practices. [Whites Agency](https://whites.agency/) focuses strongly on Data-Driven SEO. We run many Big Data analyses which give us insights into multiple optimization opportunities.
-
-Majority of cases we are dealing with right now focus on data harvesting and analysis. Data presentation plays an important part and since the beginning, we needed a tool that would allow us to experiment with different forms of visualizations. Because our organization is Python driven, Matplotlib was a straightforward choice for us. It is a mature project that offers flexibility and control. Among other features, Matplotlib figures can be easily exported not only to raster graphic formats (PNG, JPG) but also to vector ones (SVG, PDF, EPS), creating high-quality images that can be embedded in HTML code, LaTeX or utilized by graphic designers. In one of our projects, Matplotlib was a part of the Python processing pipeline that automatically generated PDF summaries from an HTML template for individual clients. Every data visualization project has the same core presented in the figure below, where data is loaded from the database, processed in pandas or PySpark and finally visualized with Matplotlib.
-
-
-
-In what follows, we would like to share two insights from our studies. All figures were prepared in Matplotlib and in each case we set up a global style (overwritten if necessary):
-```
-import matplotlib.pyplot as plt
-from cycler import cycler
-
-colors = ['#00b2b8', '#fa5e00', '#404040', '#78A3B3', '#008F8F', '#ADC9D6']
-
-plt.rc('axes', grid=True, labelcolor='k', linewidth=0.8, edgecolor='#696969',
- labelweight='medium', labelsize=18)
-plt.rc('axes.spines', left=False, right=False, top=False, bottom=True)
-plt.rc('axes.formatter', use_mathtext=True)
-
-plt.rcParams['axes.prop_cycle'] = cycler('color', colors)
-
-plt.rc('grid', alpha=1.0, color='#B2B2B2', linestyle='dotted', linewidth=1.0)
-plt.rc('xtick.major', top=False, width=0.8, size=8.0)
-plt.rc('ytick', left=False, color='k')
-plt.rcParams['xtick.color'] = 'k'
-plt.rc('font',family='Montserrat')
-plt.rcParams['font.weight'] = 'medium'
-plt.rcParams['xtick.labelsize'] = 13
-plt.rcParams['ytick.labelsize'] = 13
-plt.rcParams['lines.linewidth'] = 2.0
-```
-# Case 1: Website Speed Performance
-Our R&D department analyzed a set of 10,000 potential customer intent phrases from the *Electronics* (eCommerce) and *News* domains (5000 phrases each). They scraped data from the Google ranking in a specific location (London, United Kingdom) both for mobile and desktop results [full study available [here](https://whites.agency/blog/google-lighthouse-study-seo-ranking-factors-in-ecommerce-vs-news/)]. Based on those data, we distinguished TOP 20 results that appeared in SERPs. Next, each page was audited with the [Google Lighthouse tool](https://developers.google.com/web/tools/lighthouse). Google Lighthouse is an open-source, automated tool for improving the quality of web pages, that among other collects information about website loading time. A single sample from our analysis which shows variations of *Time to First Byte* (TTFB) as a function of Google position (grouped in threes) is presented below. TTFB measures the time it takes for a user's browser to receive the first byte of page content. Regardless of the device, TTFB score is the lowest for websites that occurred in TOP 3 positions. The difference is significant, especially between TOP 3 and 4-6 results. Therefore, Google favors websites that respond fast and therefore it is advised to invest in website speed optimization.
-
-
-
-The figure above uses `fill_between` function from Matplotlib library to draw colored shade that represents the 40-60th percentile range. A simple line plot with circle markers denotes the median (50th percentile). X-axis labels were assigned manually. The whole style is wrapped into a custom function that allows us to reproduce the whole figure in a single line of code. A sample is presented below:
-
-```
-import matplotlib.pyplot as plt
-from matplotlib.colors import LinearSegmentedColormap
-
-# --------------------------------------------
-# Set double column layout
-# --------------------------------------------
-fig, axx = plt.subplots(figsize=(20,6), ncols=2)
-
-# --------------------------------------------
-# Plot 50th percentile
-# --------------------------------------------
-line_kws = {
- 'lw': 4.0,
- 'marker': 'o',
- 'ms': 9,
- 'markerfacecolor': 'w',
- 'markeredgewidth': 2,
- 'c': '#00b2b8'
-}
-
-# just demonstration
-axx[0].plot(x, y, label='Electronics', **line_kws)
-
-# --------------------------------------------
-# Plot 40-60th percentile
-# --------------------------------------------
-# make color lighter
-cmap = LinearSegmentedColormap.from_list('whites', ['#FFFFFF', '#00b2b8'])
-
-# just demonstration
-axx[0].fill_between(
- x, yl, yu,
- color=cmap(0.5),
- label='_nolegend_'
-)
-
-# ---------------------------------------------
-# Add x-axis labels
-# ---------------------------------------------
-# done automatically
-xtick_labels = ['1-3','4-6','7-9','10-12','13-15','16-18','19-20']
-for ax in axx:
- ax.set_xticklabels(xtick_labels)
-
-# ----------------------------------------------
-# Export figure
-# ----------------------------------------------
-fig.savefig("lighthouse.png", bbox_inches='tight', dpi=250)
-```
-
-# Case 2: Google Ads ranking
-Another example let us draw insights from Google's paid campaigns (Ads). Our R&D department scraped the first page in Google for more than 7600 queries and analyzed the ads that were present [study available only in [Polish](https://agencjawhites.pl/aktualnosci/ponad-1000-graczy-walczy-o-polskiego-turyste-w-wyszukiwarce-google/)]. The queries were narrowed down to *Travel* category. At the moment of writing this post, each SERP can have up to 4 ads at the top and up to 3 ads at the bottom. Each ad is associated with a domain and has a headline, description, and optional extensions. Below we present TOP 25 domains with the highest visibility on desktop computers. The Y-axis shows the name of a domain and the X-axis indicates how many ads is linked with particular domain, in total. We repeated the study 3 times and aggregated the counts that is why the scale is much larger than 7600. In this project, the type of plot below allows us to summarize different brands' ads campaign strategies and their advertising market shares. For example, *itaka* and *wakacje* have the strongest presence both on mobile and desktop and most of their ads appear at the top. The *neckermann* positions itself are very high, but most of their ads appear at the bottom of search results.
-
-
-
-The figure above is a standard horizontal bar plot that can be reproduced with `barh` function in Matplotlib. Each y-tick has 4 different pieces (see legend). We also added automatically generated count numbers at the end of each bar for better readability. The code snippet is shown below:
-
-```
-import matplotlib.pyplot as plt
-import matplotlib.patches as mpatches
-from matplotlib.colors import LinearSegmentedColormap, PowerNorm
-
-# -----------------------------
-# Set default colors
-# -----------------------------
-blues = LinearSegmentedColormap.from_list(name='WhitesBlues', colors=['#FFFFFF', '#00B3B8'], gamma=1.0)
-oranges = LinearSegmentedColormap.from_list(name='WhitesOranges', colors=['#FFFFFF', '#FB5E01'], gamma=1.0)
-
-# colors
-desktop_top = blues(1.0)
-desktop_bottom = oranges(1.0)
-mobile_top = blues(0.5)
-mobile_bottom = oranges(0.5)
-
-# -----------------------------
-# Prepare Figure
-# -----------------------------
-fig, ax = plt.subplots(figsize=(10,15))
-ax.grid(False)
-
-# -----------------------------
-# Plot bars
-# -----------------------------
-# just demonstration
-
-for name in yticklabels:
- # tmp_desktop - DataFrame with desktop data
- # tmp_mobile - DataFrame with mobile data
-
- ax.barh(cnt, tmp_desktop['top'], color=desktop_top, height=0.9)
- ax.barh(cnt, tmp_desktop['bottom'], left=tmp_desktop['top'], color=desktop_bottom, height=0.9)
- # text counter
- ax.text(tmp_desktop['all']+100, cnt, "%d" % tmp_desktop['all'], horizontalalignment='left',
- verticalalignment='center', fontsize=10)
-
- ax.barh(cnt-1, tmp_mobile['top'], color=mobile_top, height=0.9)
- ax.barh(cnt-1, tmp_mobile['bottom'], left=tmp_mobile['top'], color=mobile_bottom, height=0.9)
- ax.text(tmp_mobile['all']+100, cnt-1, "%d" % tmp_mobile['all'], horizontalalignment='left',
- verticalalignment='center', fontsize=10)
-
-
- yticks.append(cnt)
-
- cnt = cnt - 2.5
-
-# -----------------------------
-# set labels
-# -----------------------------
-ax.set_yticks(yticks)
-ax.set_yticklabels(yticklabels)
-
-# -----------------------------
-# Add legend manually
-# -----------------------------
-legend_elements = [
- mpatches.Patch(color=desktop_top, label='desktop top'),
- mpatches.Patch(color=desktop_bottom, label='desktop bottom'),
- mpatches.Patch(color=mobile_top, label='mobile top'),
- mpatches.Patch(color=mobile_bottom, label='mobile bottom')
-]
-
-ax.legend(handles=legend_elements, fontsize=15)
-```
-# Summary
-This is just a sample from our studies and more can be found on our website. The Matplotlib library meets our needs in terms of visual capabilities and flexibility. It allows us to create standard plots in a single line of code, as well as experiment with different forms of graphs thanks to its lower level features. Thanks to opportunities offered by Matplotlib we may present the complicated data in a simple and reader-friendly way.
diff --git a/content/posts/matplotlib-rsef/index.md b/content/posts/matplotlib-rsef/index.md
deleted file mode 100644
index c2e6865..0000000
--- a/content/posts/matplotlib-rsef/index.md
+++ /dev/null
@@ -1,44 +0,0 @@
----
-title: "Elliott Sales de Andrade hired as Matplotlib Software Research Engineering Fellow"
-date: 2020-03-20T15:51:00-04:00
-draft: false
-description: "We have hired Elliott Sales de Andrade as the Matplotlib Software Research Engineering Fellow supported by the Chan Zuckerberg Initiative Essential Open Source Software for Science"
-categories: ["News"]
-author: Thomas A Caswell, Hannah Aizenman, Elliott Sales de Andrade
-displayInList: true
----
-
-
-As has been discussed in detail in Nadia Eghbal's [Roads and Bridges](https://www.fordfoundation.org/work/learning/research-reports/roads-and-bridges-the-unseen-labor-behind-our-digital-infrastructure/), the CZI EOSS [program
-announcement](https://chanzuckerberg.com/rfa/essential-open-source-software-for-science/), and in the NumFocus [sustainability program goals](https://numfocus.org/programs/sustainability), much of the critical software that science and industry are built on
-is maintained by a primarily volunteer community. While this has worked, it is not sustainable in the long term for the health of many
-projects or their contributors.
-
-We are happy to announce that we have hired Elliott Sales de Andrade ([QuLogic](https://github.com/QuLogic))
-as the [Matplotlib Software Research Engineering
-Fellow](https://github.com/matplotlib/CZI_2019-07_mpl) supported by
-the [Chan Zuckerberg Initiative Essential Open Source Software for
-Science](https://chanzuckerberg.com/eoss/proposals/matplotlib-foundation-of-scientific-visualization-in-python/)
-effective March 1, 2020!
-
-Elliott has been contributing to a broad variety of Free and Open
-Source projects for several years. He is an active Matplotlib
-contributor and has had commit rights since October 2015. In addition
-to working on Matplotlib, Elliott has contributed to a wide range of
-projects in the Scientific Python software stack, both downstream and
-upstream of Matplotlib, including
-[Cartopy](https://scitools.org.uk/cartopy/),
-[ObsPy](https://obspy.org/), and [NumPy](https://numpy.org/). Outside
-of Python, Elliott is a developer on the [Pidgin
-project](https://pidgin.im/) and a packager for [Fedora
-Linux](https://getfedora.org/). In his work on Matplotlib, he is interested in advancing
-science through reproducible workflows and more accessible libraries.
-
-We are already seeing a reduction in the backlog of open issues and
-pull requests, which we hope will make the library easier to
-contribute to and maintain long term. We also benefit from Elliott
-having the bandwidth to maintain a library wide view of all the
-on-going work and open bugs. Hiring Elliott as an RSEF is the
-start of ensuring that Matplotlib is sustainable in the long term.
-
-Looking forward to all the good work we are going to do this year!
diff --git a/content/posts/mpl-for-making-diagrams/index.md b/content/posts/mpl-for-making-diagrams/index.md
deleted file mode 100644
index cfc7680..0000000
--- a/content/posts/mpl-for-making-diagrams/index.md
+++ /dev/null
@@ -1,253 +0,0 @@
----
-title: "Matplotlib for Making Diagrams"
-date: 2020-02-19T12:57:07-05:00
-draft: false
-description: "How to use Matplotlib to make diagrams."
-categories: ["tutorials"]
-displayInList: true
-author: Brandon Rohrer
-
-resources:
-- name: featuredImage
- src: "causal.png"
- params:
- description: "A causal model diagram"
- showOnTop: true
----
-
-
-# Matplotlib for diagrams
-
-This is my first post for the Matplotlib blog so I wanted to lead
-with an example of what I most love about it:
-How much control Matplotlib gives you.
-I like to use it as a programmable drawing tool that happens
-to be good at plotting data.
-
-The default layout for Matplotlib works great for a lot of things,
-but sometimes you want to exert
-more control. Sometimes you want to treat your figure window as
-a blank canvas and create diagrams
-to communicate your ideas. Here, we will walk through the process
-for setting this up. Most of these tricks are detailed in
-[this cheat sheet for laying out plots](https://e2eml.school/matplotlib_framing.html).
-
-
-```python
-import matplotlib.pyplot as plt
-import numpy as np
-```
-
-The first step is to choose the size of your canvas.
-
-(Just a heads up, I love the metaphor
-of the canvas, so that's how I am using the term here.
-The Canvas object is a very specific
-thing in the Matplotlib code base. That's not what I'm referring to.)
-
-I'm planning to make a diagram that is 16 centimeters wide
-and 9 centimeters high.
-This will fit comfortably on a piece of A4 or US Letter paper
-and will be almost twice as wide as it is high.
-It also scales up nicely to fit on a wide-format slide presentation.
-
-The `plt.figure()` function accepts a `figsize` argument,
-a tuple of `(width, height)` in **inches**.
-To convert from centimeters, we'll divide by 2.54.
-
-```python
-fig_width = 16 # cm
-fig_height = 9 # cm
-fig = plt.figure(figsize=(fig_width / 2.54, fig_height / 2.54))
-```
-
-The next step is to add an Axes object that we can draw on.
-By default, Matplotlib will size and place the Axes to leave
-a little border and room for x- and y-axis labels. However, we don't
-want that this time around. We want our Axes to extend right up
-to the edge of the Figure.
-
-The `add_axes()` function lets us specify exactly where to place
-our new Axes and how big to make it. It accepts a tuple of the format
-`(left, bottom, width, height)`. The coordinate frame of the Figure
-is always (0, 0) at the bottom left corner and (1, 1) at the upper right,
-no matter what size of Figure you are working with. Positions, widths,
-and heights all become fractions of the total width and height of the Figure.
-
-To fill the Figure with our Axes entirely, we specify a left position of 0,
-a bottom position of 0, a width of 1, and a height of 1.
-
-```python
-ax = fig.add_axes((0, 0, 1, 1))
-```
-
-To make our diagram creation easier, we can set the axis limits so that
-one unit in the figure equals one centimeter. This grants us
-an intuitive way to control the size of objects in the diagram.
-A circle with a radius of 2 will be drawn as a circle (not an ellipse)
-in the final image and have a radius of 2 cm.
-
-```python
-ax.set_xlim(0, fig_width)
-ax.set_ylim(0, fig_height)
-```
-
-We can also do away with the automatically generated ticks
-and tick labels with this pair of calls.
-
-```python
-ax.tick_params(bottom=False, top=False, left=False, right=False)
-ax.tick_params(labelbottom=False, labeltop=False, labelleft=False, labelright=False)
-```
-
-At this point we have a big blank space of exactly the right size and shape.
-Now we can begin building our diagram. The foundation of the image will be
-the background color. White is fine, but sometimes it's fun to mix it up.
-[Here are some ideas](https://e2eml.school/matplotlib_lines.html#color)
-to get you started.
-
-```python
-ax.set_facecolor("antiquewhite")
-```
-
-We can also add a border to the diagram to visually set it apart.
-
-```python
-ax.spines["top"].set_color("midnightblue")
-ax.spines["bottom"].set_color("midnightblue")
-ax.spines["left"].set_color("midnightblue")
-ax.spines["right"].set_color("midnightblue")
-ax.spines["top"].set_linewidth(4)
-ax.spines["bottom"].set_linewidth(4)
-ax.spines["left"].set_linewidth(4)
-ax.spines["right"].set_linewidth(4)
-```
-
-Now we have a foundation and background in place
-and we're finally ready to start drawing.
-You have complete freedom to
-[draw curves and shapes](https://e2eml.school/matplotlib_lines.html),
-[place points](https://e2eml.school/matplotlib_points.html),
-and [add text](https://e2eml.school/matplotlib_text.html)
-of any variety within our 16 x 9 garden walls.
-
-Then when you're done, the last step is to save the figure out as a
-`.png` file. In this format it can be imported to and added to whatever
-document or presentation you're working on
-
-```python
-fig.savefig("blank_diagram.png", dpi=300)
-```
-
-
-
-If you're making a collection of diagrams,
-you can make a convenient template for your blank canvas.
-
-```python
-def blank_diagram(fig_width=16, fig_height=9,
- bg_color="antiquewhite", color="midnightblue"):
- fig = plt.figure(figsize=(fig_width / 2.54, fig_height / 2.54))
- ax = fig.add_axes((0, 0, 1, 1))
- ax.set_xlim(0, fig_width)
- ax.set_ylim(0, fig_height)
- ax.set_facecolor(bg_color)
-
- ax.tick_params(bottom=False, top=False,
- left=False, right=False)
- ax.tick_params(labelbottom=False, labeltop=False,
- labelleft=False, labelright=False)
-
- ax.spines["top"].set_color(color)
- ax.spines["bottom"].set_color(color)
- ax.spines["left"].set_color(color)
- ax.spines["right"].set_color(color)
- ax.spines["top"].set_linewidth(4)
- ax.spines["bottom"].set_linewidth(4)
- ax.spines["left"].set_linewidth(4)
- ax.spines["right"].set_linewidth(4)
-
- return fig, ax
-```
-
-Then you can take that canvas and add arbitrary text, shapes, and lines.
-
-```python
-fig, ax = blank_diagram()
-
-for x0 in np.arange(-3, 16, .5):
- ax.plot([x0, x0 + 3], [0, 9], color="black")
-
-fig.savefig("stripes.png", dpi=300)
-```
-
-
-
-Or more intricately:
-
-```python
-fig, ax = blank_diagram()
-
-centers = [(3.5, 6.5), (8, 6.5), (12.5, 6.5), (8, 2.5)]
-radii = 1.5
-texts = [
- "\n".join(["My roommate", "is a Philistine", "and a boor"]),
- "\n".join(["My roommate", "ate the last", "of the", "cold cereal"]),
- "\n".join(["I am really", "really hungy"]),
- "\n".join(["I'm annoyed", "at my roommate"]),
-]
-
-# Draw circles with text in the center
-for i, center in enumerate(centers):
- x, y = center
- theta = np.linspace(0, 2 * np.pi, 100)
- ax.plot(
- x + radii * np.cos(theta),
- y + radii * np.sin(theta),
- color="midnightblue",
- )
- ax.text(
- x, y,
- texts[i],
- horizontalalignment="center",
- verticalalignment="center",
- color="midnightblue",
- )
-
-# Draw arrows connecting them
-# https://e2eml.school/matplotlib_text.html#annotate
-ax.annotate(
- "",
- (centers[1][0] - radii, centers[1][1]),
- (centers[0][0] + radii, centers[0][1]),
- arrowprops=dict(arrowstyle = "-|>"),
-)
-ax.annotate(
- "",
- (centers[2][0] - radii, centers[2][1]),
- (centers[1][0] + radii, centers[1][1]),
- arrowprops=dict(arrowstyle = "-|>"),
-)
-ax.annotate(
- "",
- (centers[3][0] - .7 * radii, centers[3][1] + .7 * radii),
- (centers[0][0] + .7 * radii, centers[0][1] - .7 * radii),
- arrowprops=dict(arrowstyle = "-|>"),
-)
-ax.annotate(
- "",
- (centers[3][0] + .7 * radii, centers[3][1] + .7 * radii),
- (centers[2][0] - .7 * radii, centers[2][1] - .7 * radii),
- arrowprops=dict(arrowstyle = "-|>"),
-)
-
-fig.savefig("causal.png", dpi=300)
-```
-
-
-
-Once you get started on this path, you can start making
-extravagantly annotated plots. It can elevate your data
-presentations to true storytelling.
-
-Happy diagram building!
diff --git a/content/posts/pyplot-vs-object-oriented-interface/index.md b/content/posts/pyplot-vs-object-oriented-interface/index.md
deleted file mode 100644
index 290fc0f..0000000
--- a/content/posts/pyplot-vs-object-oriented-interface/index.md
+++ /dev/null
@@ -1,209 +0,0 @@
----
-title: "Pyplot vs Object Oriented Interface"
-date: 2020-05-27T20:21:30+05:30
-draft: false
-description: "This post describes the difference between the pyplot and object oriented interface to make plots."
-author: Tejas Sanap
-displayInList: true
-resources:
-- name: featuredImage
- src: "figure/distance-and-velocity-different-axes-finished.png"
- params:
- description: "Finished graph"
- showOnTop: true
----
-
-## Generating the data points
-
-To get acquainted with the basics of plotting with `matplotlib`, let's try plotting how much distance an object under free-fall travels with respect to time and also, its velocity at each time step.
-
-If, you have ever studied physics, you can tell that is a classic case of Newton's equations of motion, where
-
-$$ v = a \times t $$
-
-$$ S = 0.5 \times a \times t^{2} $$
-
-We will assume an initial velocity of zero.
-
-```python
-import numpy as np
-
-time = np.arange(0., 10., 0.2)
-velocity = np.zeros_like(time, dtype=float)
-distance = np.zeros_like(time, dtype=float)
-```
-
-We know that under free-fall, all objects move with the constant acceleration of $$g = 9.8~m/s^2$$
-
-```python
-g = 9.8 # m/s^2
-
-velocity = g * time
-distance = 0.5 * g * np.power(time, 2)
-```
-
-The above code gives us two `numpy` arrays populated with the distance and velocity data points.
-
-## Pyplot vs. Object-Oriented interface
-
-When using `matplotlib` we have two approaches:
-1. `pyplot` interface / functional interface.
-2. Object-Oriented interface (OO).
-
-### Pyplot Interface
-
-`matplotlib` on the surface is made to imitate MATLAB's method of generating plots, which is called `pyplot`. All the `pyplot` commands make changes and modify the same figure. This is a state-based interface, where the state (i.e., the figure) is preserved through various function calls (i.e., the methods that modify the figure). This interface allows us to quickly and easily generate plots. The state-based nature of the interface allows us to add elements and/or modify the plot as we need, when we need it.
-
-This interface shares a lot of similarities in syntax and methodology with MATLAB. For example, if we want to plot a blue line where each data point is marked with a circle, we can use the string `'bo-'`.
-
-```python
-import matplotlib.pyplot as plt
-
-plt.figure(figsize=(9,7), dpi=100)
-plt.plot(time,distance,'bo-')
-plt.xlabel("Time")
-plt.ylabel("Distance")
-plt.legend(["Distance"])
-plt.grid(True)
-```
-
-The plot shows how much distance was covered by the free-falling object with each passing second.
-
-
-A tutorial on how to create custom tables in Matplotlib which allow for flexible design and customization.
Posted
#tutorials
UNC BIOL222: Art created with Matplotlib
Posted
#art #academia
New open access book released
Posted
#News
A tutorial on how to show usage rates and more using batteries
Posted
#tutorials
Advocating is all about communicating facts clearly. I used Matplotlib to show the financial struggles of postdocs in the Boston area.
Posted
#academia
See how you can contribute to the matplotblog.
Posted
#tutorials
Matplotblog, the new blog of Matplotlib, to showcase and share great visualization stories.
Posted
#editorial
Google Summer of Code 2021: Final Report - Aitik Gupta
Posted
#News #GSoC
Quarter Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
The Python Graph Gallery is a website that displays hundreds of chart examples made with python. It goes from very basic to highly customized examples and is based on common viz libraries like matplotlib, seaborn or plotly.
Posted
#tutorials #graphs
Pre-Quarter Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
Mid-Term Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
Introduction about Aitik Gupta, Google Summer of Code 2021 Intern under the parent organisation: NumFOCUS
Posted
#News #GSoC
Learn how to create a simple stellar chart, an alternative to the radar chart.
Posted
#tutorials
Many figures in the IPCC SR15 were generated using Matplotlib. +The data and open-source notebooks were published to increase the transparency and reproducibility of the analysis.
Posted
#academia #tutorials
This is my first post contribution to Matplotlib.
Posted
#GSoD
Learn how to easily create step charts through examining the multilingualism of pop group WayV
Posted
#tutorials #graphs
Final Work Product Report for the Google Summer of Code 2020 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the first half of the Google Summer of Code 2020 Phase 3 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the second half of the Google Summer of Code 2020 Phase 2 for the Baseline Images Problem
Posted
#News #GSoC
A brief tour through the world of elementary cellular automata
Posted
#tutorials
Progress Report for the first half of the Google Summer of Code 2020 Phase 2 for the Baseline Images Problem
Posted
#News #GSoC
Discover the bizarre geometry of the fractals and learn how to make an animated visualization of these marvels using Python and the Matplotlib's Animation API.
Posted
#tutorials
Progress Report for the second half of the Google Summer of Code 2020 Phase 1 for the Baseline Images Problem
Posted
#News #GSoC
This post describes how to animate some oceanographic measurements in a tweaked polar plot
Posted
#tutorials
Progress Report for the first half of the Google Summer of Code 2020 Phase 1 for the Baseline Images Problem
Posted
#News #GSoC
This post describes the difference between the pyplot and object oriented interface to make plots.
Posted
Applied image manipulation to create procedural art.
Posted
#tutorials #art
A fun project about drawing all possible differently-looking (not isomorphic) graphs of N nodes.
Posted
#tutorials #graphs
Introductory post about Sidharth Bansal, Google Summer of Code 2020 Intern for Baseline Image Problem Project under Numfocus
Posted
#News #GSoC
Futuristic neon glow for your next data visualization
Posted
#tutorials
We have hired Elliott Sales de Andrade as the Matplotlib Software Research Engineering Fellow supported by the Chan Zuckerberg Initiative Essential Open Source Software for Science
Posted
#News
How to use Matplotlib to make diagrams.
Posted
#tutorials
This post details how to leverage gridspec to create ridgeplots in Matplotlib
Posted
#tutorials
Learn how to create a Tesla Cybertruck with Matplotlib that drives via animation.
Posted
#tutorials
This guide dives deep into the inner workings of Matplotlib's Figures, Axes, subplots and the very amazing GridSpec!
Posted
#tutorials
3D rendering is really easy once you've understood a few concepts. To demonstrate that, we'll design a simple custom 3D engine that with 60 lines of Python and one Matplotlib call. That is, we'll render the bunny without using the 3D axis.
Posted
#tutorials #3D
At Whites Agency we analyze big unstructured data to increases client's online visibility. We share our story of how we used Matplotlib to present the complicated data in a simple and reader-friendly way.
Posted
#industry
Ed Hawkins made this impressively simple plot to show how global temperatures have risen since 1880. Here is how to recreate it using Matplotlib.
Posted
#tutorials #academia
Posted
Matplotlib is an open-source Python visualization library. As such, there are a multitude of contributors and users that assist in improving Matplotlib and expanding its reach every day. They have helped it to become what it is and help show the world what is possible with a (relatively) little Python code.
To further help Matplotlib users make impressive visualizations and to ultimately tell impactful stories with their data, we have created this blog. This new site will be home to news affecting the Matplotlib community, tutorials, and other relevant content.
It is our hope that as we continue to move forward with the project, Matplotlib users will enjoy and derive much benefit from the posts contained here.
Posted +
# This is specific to Jupyter Notebooks
+%matplotlib inline
+import numpy as np
+import matplotlib.pyplot as plt
+import matplotlib as mpl
+A Top-Down runnable Jupyter Notebook with the exact contents of this blog can be found here
An interactive version of this guide can be accessed on Google Colab
Although a beginner can follow along with this guide, it is primarily meant for people who have at least a basic knowledge of how Matplotlib's plotting functionality works.
Essentially, if you know how to take 2 NumPy arrays and plot them (using an appropriate type of graph) on 2 different axes in a single figure and give it basic styling, you're good to go for the purposes of this guide.
If you feel you need some introduction to basic Matplotlib plotting, here's a great guide that can help you get a feel for introductory plotting using Matplotlib : https://matplotlib.org/devdocs/gallery/subplots_axes_and_figures/subplots_demo.html
From here on, I will be assuming that you have gained sufficient knowledge to follow along this guide.
Also, in order to save everyone's time, I will keep my explanations short, terse and very much to the point, and sometimes leave it for the reader to interpret things (because that's what I've done throughout this guide for myself anyway).
The primary driver in this whole exercise will be code and not text, and I encourage you to spin up a Jupyter notebook and type in and try out everything yourself to make the best use of this resource.
This is not a guide about how to beautifully plot different kinds of data using Matplotlib, the internet is more than full of such tutorials by people who can explain it way better than I can.
This article attempts to explain the workings of some of the foundations of any plot you create using Matplotlib. +We will mostly refrain from focusing on what data we are plotting and instead focus on the anatomy of our plots.
Matplotlib has many styles available, we can see the available options using:
plt.style.available
+['seaborn-dark',
+ 'seaborn-darkgrid',
+ 'seaborn-ticks',
+ 'fivethirtyeight',
+ 'seaborn-whitegrid',
+ 'classic',
+ '_classic_test',
+ 'fast',
+ 'seaborn-talk',
+ 'seaborn-dark-palette',
+ 'seaborn-bright',
+ 'seaborn-pastel',
+ 'grayscale',
+ 'seaborn-notebook',
+ 'ggplot',
+ 'seaborn-colorblind',
+ 'seaborn-muted',
+ 'seaborn',
+ 'Solarize_Light2',
+ 'seaborn-paper',
+ 'bmh',
+ 'tableau-colorblind10',
+ 'seaborn-white',
+ 'dark_background',
+ 'seaborn-poster',
+ 'seaborn-deep']
+We shall use seaborn. This is done like so:
plt.style.use('seaborn')
+Let's get started!
# Creating some fake data for plotting
+xs = np.linspace(0, 2 * np.pi, 400)
+ys = np.sin(xs ** 2)
+
+xc = np.linspace(0, 2 * np.pi, 600)
+yc = np.cos(xc ** 2)
+The usual way to create a plot using Matplotlib goes somewhat like this:
fig, ax = plt.subplots(2, 2, figsize=(16, 8))
+# `Fig` is short for Figure. `ax` is short for Axes.
+ax[0, 0].plot(xs, ys)
+ax[1, 1].plot(xs, ys)
+ax[0, 1].plot(xc, yc)
+ax[1, 0].plot(xc, yc)
+fig.suptitle("Basic plotting using Matplotlib")
+plt.show()
+
Our goal today is to take apart the previous snippet of code and understand all of the underlying building blocks well enough so that we can use them separately and in a much more powerful way.
If you're a beginner like I was before writing this guide, let me assure you: this is all very simple stuff.
Going into plt.subplots documentation (hit Shift+Tab+Tab in a Jupyter notebook) reveals some of the other Matplotlib internals that it uses in order to give us the Figure and it's Axes.
These include :
plt.subplotplt.figurempl.figure.Figurempl.figure.Figure.add_subplotmpl.gridspec.GridSpecmpl.axes.AxesLet's try and figure out what these functions / classes do.
Figure? And what are Axes?A Figure in Matplotlib is simply your main (imaginary) canvas. This is where you will be doing all your plotting / drawing / putting images and what not. This is the central object with which you will always be interacting. A figure has a size defined for it at the time of creation.
You can define a figure like so (both statements are equivalent):
fig = mpl.figure.Figure(figsize=(10,10))
+# OR
+fig = plt.figure(figsize=(10,10))
+Notice the word imaginary above. What this means is that a Figure by itself does not have any place for you to plot. You need to attach/add an Axes to it to do any kind of plotting. You can put as many Axes objects as you want inside of any Figure you have created.
An Axes:
FigureFigure.You can create an Axes like so (both statements are equivalent):
ax1 = mpl.axes.Axes(fig=fig, rect=[0,0,0.8,0.8], facecolor='red')
+#OR
+ax1 = plt.Axes(fig=fig, rect=[0,0,0.8,0.8], facecolor='red')
+#
+The first parameter fig is simply a pointer to the parent Figure to which an Axes will belong.
The second parameter rect has four numbers : [left_position, bottom_position, height, width] to define the position of the Axes inside the Figure and the height and width with respect to the Figure. All these numbers are expressed in percentages.
A Figure simply holds a given number of Axes at any point of time
We will go into some of these design decisions in a few moments’
plt.subplots with basic Matplotlib functionalityWe will try and recreate the below plot using Matplotlib primitives as a way to understand them better. We'll try and be a slightly creative by deviating a bit though.
fig, ax = plt.subplots(2,2)
+fig.suptitle("2x2 Grid")
+Text(0.5, 0.98, '2x2 Grid')
+
# We first need a figure, an imaginary canvas to put things on
+fig = plt.Figure(figsize=(6,6))
+# Let's start with two Axes with an arbitrary position and size
+ax1 = plt.Axes(fig=fig, rect=[0.3, 0.3, 0.4, 0.4], facecolor='red')
+ax2 = plt.Axes(fig=fig, rect=[0, 0, 1, 1], facecolor='blue')
+Now you need to add the Axes to fig. You should stop right here and think about why would there be a need to do this when fig is already a parent of ax1 and ax2? Let's do this anyway and we'll go into the details afterwards.
fig.add_axes(ax2)
+fig.add_axes(ax1)
+<matplotlib.axes._axes.Axes at 0x1211dead0>
+# As you can see the Axes are exactly where we specified.
+fig
+
That means you can do this now:
Remark: Notice the
ax.reverse()call in the snippet below. If I hadn't done that, the biggest plot would be placed in the end on top of every other plot and you would just see a single, blank ‘cyan’ colored plot.
fig = plt.figure(figsize=(6,6))
+ax = []
+sizes = np.linspace(0.02, 1, 50)
+for i in range(50):
+ color = str(hex(int(sizes[i] * 255)))[2:]
+ if len(color) == 1: color = '0' + color
+ color = '#99' + 2 * color
+ ax.append(plt.Axes(fig=fig, rect=[0,0, sizes[i], sizes[i]], facecolor=color))
+
+ax.reverse()
+for axes in ax:
+ fig.add_axes(axes)
+plt.show()
+
The above example demonstrates why it is important to decouple the process of creation of an Axes and actually putting it onto a Figure.
Also, you can remove an Axes from the canvas area of a Figure like so:
fig.delaxes(ax)
+This can be useful when you want to compare the same primary data (GDP) to several secondary data sources (education, spending, etc.) one by one (you'll need to add and delete each graph from the Figure in succession)
I also encourage you to look into the documentation for Figure and Axes and glance over the several methods available to them. This will help you know what parts of the wheel you do not need to rebuild when you're working with these objects the next time.
This should now make sense. We can now create our original plt.subplots(2, 2) example using the knowledge we have thus gained so far.
(Although, this is definitely not the most convenient way to do this)
fig = mpl.figure.Figure(); fig
+
+fig.suptitle("Recreating plt.subplots(2, 2)")
+
+ax1 = mpl.axes.Axes(fig=fig, rect=[0,0,0.42,0.42])
+ax2 = mpl.axes.Axes(fig=fig, rect=[0, 0.5, 0.42, 0.42])
+ax3 = mpl.axes.Axes(fig=fig, rect=[0.5,0,0.42,0.42])
+ax4 = mpl.axes.Axes(fig=fig, rect=[0.5, 0.5, 0.42, 0.42])
+
+fig.add_axes(ax1)
+fig.add_axes(ax2)
+fig.add_axes(ax3)
+fig.add_axes(ax4)
+
+fig
+
gridspec.GridSpecDocs : https://matplotlib.org/api/_as_gen/matplotlib.gridspec.GridSpec.html#matplotlib.gridspec.GridSpec
GridSpec objects allow us more intuitive control over how our plot is exactly divided into subplots and what the size of each Axes is.
You can essentially decide a Grid which all your Axes will conform to when laying themselves over.
Once you define a grid, or GridSpec so to say, you can use that object to generate new Axes conforming to the grid which you can then add to your Figure
Lets see how all of this works in code:
You can define a GridSpec object like so (both statements are equivalent):
gs = mpl.gridspec.GridSpec(nrows, ncols, width_ratios, height_ratios)
+# OR
+gs = plt.GridSpec(nrows, ncols, width_ratios, height_ratios)
+More specifically:
gs = plt.GridSpec(nrows=3, ncols=3, width_ratios=[1,2,3], height_ratios[3,2,1])
+nrows and ncols are pretty self explanatory. width_ratios determines the relative width of each column. height_ratios follows along the same lines.
+The whole grid will always distribute itself using all the space available to it inside of a figure (things change up a bit when you have multiple GridSpec objects for a single figure, but that's for you to explore!). And inside of a grid, all the Axes will conform to the sizes and ratios defined already
def annotate_axes(fig):
+ """Taken from https://matplotlib.org/gallery/userdemo/demo_gridspec03.html#sphx-glr-gallery-userdemo-demo-gridspec03-py
+ takes a figure and puts an 'axN' label in the center of each Axes
+ """
+ for i, ax in enumerate(fig.axes):
+ ax.text(0.5, 0.5, "ax%d" % (i+1), va="center", ha="center")
+ ax.tick_params(labelbottom=False, labelleft=False)
+fig = plt.figure()
+
+# We will try and vary axis sizes here just to see what happens
+gs = mpl.gridspec.GridSpec(nrows=2, ncols=2, width_ratios=[1, 2], height_ratios=[4, 1])
+<Figure size 576x396 with 0 Axes>
+You can pass GridSpec objects to a Figure to create subplots in your desired sizes and proportions like so :
Notice how the sizes of the Axes relates to the ratios we defined when creating the Grid.
fig.clear()
+ax1, ax2, ax3, ax4 = [fig.add_subplot(gs[0]),
+ fig.add_subplot(gs[1]),
+ fig.add_subplot(gs[2]),
+ fig.add_subplot(gs[3])]
+
+annotate_axes(fig)
+fig
+
Doing the same thing in a simpler way
def add_gs_to_fig(fig, gs):
+ "Adds all `SubplotSpec`s in `gs` to `fig`"
+ for g in gs: fig.add_subplot(g)
+fig.clear()
+add_gs_to_fig(fig, gs)
+annotate_axes(fig)
+fig
+
That means you can now do this:
(Notice how the Axes sizes increase from top-left to bottom-right)
fig = plt.figure(figsize=(14,10))
+length = 6
+gs = plt.GridSpec(nrows=length, ncols=length,
+ width_ratios=list(range(1, length+1)), height_ratios=list(range(1, length+1)))
+
+add_gs_to_fig(fig, gs)
+annotate_axes(fig)
+for ax in fig.axes:
+ ax.plot(xs, ys)
+plt.show()
+
Notice how after each print operation, different addresses get printed for each gs object.
gs[0], gs[1], gs[2], gs[3]
+(<matplotlib.gridspec.SubplotSpec at 0x1282a9e50>,
+ <matplotlib.gridspec.SubplotSpec at 0x12942add0>,
+ <matplotlib.gridspec.SubplotSpec at 0x12942a750>,
+ <matplotlib.gridspec.SubplotSpec at 0x12a727e10>)
+gs[0], gs[1], gs[2], gs[3]
+(<matplotlib.gridspec.SubplotSpec at 0x127d5c6d0>,
+ <matplotlib.gridspec.SubplotSpec at 0x12b6d0b10>,
+ <matplotlib.gridspec.SubplotSpec at 0x129fc6390>,
+ <matplotlib.gridspec.SubplotSpec at 0x129fc6a50>)
+print(gs[0,0], gs[0,1], gs[1, 0], gs[1, 1])
+<matplotlib.gridspec.SubplotSpec object at 0x12951a610> <matplotlib.gridspec.SubplotSpec object at 0x12951a890> <matplotlib.gridspec.SubplotSpec object at 0x12951ac10> <matplotlib.gridspec.SubplotSpec object at 0x12951a150>
+print(gs[0,0], gs[0,1], gs[1, 0], gs[1, 1])
+<matplotlib.gridspec.SubplotSpec object at 0x128fad4d0> <matplotlib.gridspec.SubplotSpec object at 0x1291ebbd0> <matplotlib.gridspec.SubplotSpec object at 0x1294f9850> <matplotlib.gridspec.SubplotSpec object at 0x128106250>
+Lets understand why this happens:
Notice how a group of gs objects indexed into at the same time also produces just one object instead of multiple objects
gs[:,:], gs[:, 0]
+# both output just one object each
+(<matplotlib.gridspec.SubplotSpec at 0x128116e50>,
+ <matplotlib.gridspec.SubplotSpec at 0x128299290>)
+# Lets try another `gs` object, this time a little more crowded
+# I chose the ratios randomly
+gs = mpl.gridspec.GridSpec(nrows=3, ncols=3, width_ratios=[1, 2, 1], height_ratios=[4, 1, 3])
+All these operations print just one object. What is going on here?
print(gs[:,0])
+print(gs[1:,:2])
+print(gs[:,:])
+<matplotlib.gridspec.SubplotSpec object at 0x12a075fd0>
+<matplotlib.gridspec.SubplotSpec object at 0x128cf0990>
+<matplotlib.gridspec.SubplotSpec object at 0x12a075fd0>
+Let's try and add subplots to our Figure to see what's going on.
We'll do a few different permutations to get an exact idea.
fig = plt.figure(figsize=(5,5))
+ax1 = fig.add_subplot(gs[:2, 0])
+ax2 = fig.add_subplot(gs[2, 0])
+ax3 = fig.add_subplot(gs[:, 1:])
+annotate_axes(fig)
+
fig = plt.figure(figsize=(5,5))
+# ax1 = fig.add_subplot(gs[:2, 0])
+ax2 = fig.add_subplot(gs[2, 0])
+ax3 = fig.add_subplot(gs[:, 1:])
+annotate_axes(fig)
+
fig = plt.figure(figsize=(5,5))
+# ax1 = fig.add_subplot(gs[:2, 0])
+# ax2 = fig.add_subplot(gs[2, 0])
+ax3 = fig.add_subplot(gs[:, 1:])
+annotate_axes(fig)
+
fig = plt.figure(figsize=(5,5))
+# ax1 = fig.add_subplot(gs[:2, 0])
+# ax2 = fig.add_subplot(gs[2, 0])
+ax3 = fig.add_subplot(gs[:, 1:])
+
+# Notice the line below : You can overlay Axes using `GridSpec` too
+ax4 = fig.add_subplot(gs[2:, 1:])
+ax4.set_facecolor('orange')
+annotate_axes(fig)
+
fig.clear()
+add_gs_to_fig(fig, gs)
+annotate_axes(fig)
+fig
+
Here's a bullet point summary of what this means:
gs can be used as a sort of a factory for different kinds of Axes.factory an order by indexing into particular areas of the Grid. It gives back a single SubplotSpec (check type(gs[0]) object that helps you create an Axes which has all of the area you indexed into combined into one unit.height and width ratios for the indexed portion will determine the size of the Axes that gets generated.Axes will maintain relative proportions according to your height and width ratios always.GridSpec!This ability to create different grid variations that GridSpec provides is probably the reason for that anomaly we saw a while ago (printing different Addresses).
It creates new objects every time you index into it because it will be very troublesome to store all permutations of SubplotSpec objects into one group in memory (try and count permutations for a GridSpec of 10x10 and you'll know why)
plt.subplots(2,2) once again using GridSpecfig = plt.figure()
+gs = mpl.gridspec.GridSpec(nrows=2, ncols=2)
+add_gs_to_fig(fig, gs)
+annotate_axes(fig)
+fig.suptitle("We're done!")
+print("yayy")
+yayy
+
Here's a few things I think you should go ahead and explore:
GridSpec objects for the Same Figure.Axes effectively and meaningfully.mpl.figure.Figure and mpl.axes.Axes allowing us to manipulate their properties.seaborn, plotly, pandas and altair with much more flexibility (you can pass an Axes object to all their plotting functions). I encourage you to explore these libraries too.This is the first time I've written any technical guide for the internet, it may not be as clean as tutorials generally are. But, I'm open to all the constructive criticism that you may have for me (drop me an email on akashpalrecha@gmail.com)
Posted +
Imagine zooming an image over and over and never go out of finer details. It may sound bizarre but the mathematical +concept of fractals opens the realm towards this intricating infinity. This +strange geometry exhibits the same or similar patterns irrespectively of the scale. We can see one fractal example +in the image above.
The fractals may seem difficult to understand due to their peculiarity, but that's not the case. As Benoit Mandelbrot, +one of the founding fathers of the fractal geometry said in his legendary +TED Talk:
A surprising aspect is that the rules of this geometry are extremely short. You crank the formulas several times and +at the end, you get things like this (pointing to a stunning plot)
– Benoit Mandelbrot
In this tutorial blog post, we will see how to construct fractals in Python and animate them using the amazing +Matplotlib's Animation API. First, we will demonstrate the convergence of the Mandelbrot Set with an +enticing animation. In the second part, we will analyze one interesting property of the Julia Set. Stay tuned!
We all have a common sense of the concept of similarity. We say two objects are similar to each other if they share +some common patterns.
This notion is not only limited to a comparison of two different objects. We can also compare different parts of the +same object. For instance, a leaf. We know very well that the left side matches exactly the right side, i.e. the leaf +is symmetrical.
In mathematics, this phenomenon is known as self-similarity. It means +a given object is similar (completely or to some extent) to some smaller part of itself. One remarkable example is the +Koch Snowflake as shown in the image below:
We can infinitely magnify some part of it and the same pattern will repeat over and over again. This is how fractal +geometry is defined.
Mandelbrot Set is defined over the set of complex numbers. It consists +of all complex numbers c, such that the sequence zᵢ₊ᵢ = zᵢ² + c, z₀ = 0 is bounded. It means, after a certain +number of iterations the absolute value must not exceed a given limit. At first sight, it might +seem odd and simple, but in fact, it has some mind-blowing properties.
The Python implementation is quite straightforward, as given in the code snippet below:
def mandelbrot(x, y, threshold):
+ """Calculates whether the number c = x + i*y belongs to the
+ Mandelbrot set. In order to belong, the sequence z[i + 1] = z[i]**2 + c
+ must not diverge after 'threshold' number of steps. The sequence diverges
+ if the absolute value of z[i+1] is greater than 4.
+
+ :param float x: the x component of the initial complex number
+ :param float y: the y component of the initial complex number
+ :param int threshold: the number of iterations to considered it converged
+ """
+ # initial conditions
+ c = complex(x, y)
+ z = complex(0, 0)
+
+ for i in range(threshold):
+ z = z**2 + c
+ if abs(z) > 4.: # it diverged
+ return i
+
+ return threshold - 1 # it didn't diverge
+As we can see, we set the maximum number of iterations encoded in the variable threshold. If the magnitude of the
+sequence at some iteration exceeds 4, we consider it as diverged (c does not belong to the set) and return the
+iteration number at which this occurred. If this never happens (c belongs to the set), we return the maximum
+number of iterations.
We can use the information about the number of iterations before the sequence diverges. All we have to do +is to associate this number to a color relative to the maximum number of loops. Thus, for all complex numbers +c in some lattice of the complex plane, we can make a nice animation of the convergence process as a function +of the maximum allowed iterations.
One particular and interesting area is the 3x3 lattice starting at position -2 and -1.5 for the real and +imaginary axis respectively. We can observe the process of convergence as the number of allowed iterations increases. +This is easily achieved using the Matplotlib's Animation API, as shown with the following code:
import numpy as np
+import matplotlib.pyplot as plt
+import matplotlib.animation as animation
+
+x_start, y_start = -2, -1.5 # an interesting region starts here
+width, height = 3, 3 # for 3 units up and right
+density_per_unit = 250 # how many pixles per unit
+
+# real and imaginary axis
+re = np.linspace(x_start, x_start + width, width * density_per_unit )
+im = np.linspace(y_start, y_start + height, height * density_per_unit)
+
+fig = plt.figure(figsize=(10, 10)) # instantiate a figure to draw
+ax = plt.axes() # create an axes object
+
+def animate(i):
+ ax.clear() # clear axes object
+ ax.set_xticks([], []) # clear x-axis ticks
+ ax.set_yticks([], []) # clear y-axis ticks
+
+ X = np.empty((len(re), len(im))) # re-initialize the array-like image
+ threshold = round(1.15**(i + 1)) # calculate the current threshold
+
+ # iterations for the current threshold
+ for i in range(len(re)):
+ for j in range(len(im)):
+ X[i, j] = mandelbrot(re[i], im[j], threshold)
+
+ # associate colors to the iterations with an iterpolation
+ img = ax.imshow(X.T, interpolation="bicubic", cmap='magma')
+ return [img]
+
+anim = animation.FuncAnimation(fig, animate, frames=45, interval=120, blit=True)
+anim.save('mandelbrot.gif',writer='imagemagick')
+We make animations in Matplotlib using the FuncAnimation function from the Animation API. We need to specify
+the figure on which we draw a predefined number of consecutive frames. A predetermined interval expressed in
+milliseconds defines the delay between the frames.
In this context, the animate function plays a central role, where the input argument is the frame number, starting
+from 0. It means, in order to animate we always have to think in terms of frames. Hence, we use the frame number
+to calculate the variable threshold which is the maximum number of allowed iterations.
To represent our lattice we instantiate two arrays re and im: the former for the values on the real axis
+and the latter for the values on the imaginary axis. The number of elements in these two arrays is defined by
+the variable density_per_unit which defines the number of samples per unit step. The higher it is, the better
+quality we get, but at a cost of heavier computation.
Now, depending on the current threshold, for every complex number c in our lattice, we calculate the number of
+iterations before the sequence zᵢ₊ᵢ = zᵢ² + c, z₀ = 0 diverges. We save them in an initially empty matrix called X.
+In the end, we interpolate the values in X and assign them a color drawn from a prearranged colormap.
After cranking the animate function multiple times we get a stunning animation as depicted below:
The Julia Set is quite similar to the Mandelbrot Set. Instead of setting +z₀ = 0 and testing whether for some complex number c = x + i*y the sequence zᵢ₊ᵢ = zᵢ² + c is bounded, we +switch the roles a bit. We fix the value for c, we set an arbitrary initial condition z₀ = x + i*y, and we +observe the convergence of the sequence. The Python implementation is given below:
def julia_quadratic(zx, zy, cx, cy, threshold):
+ """Calculates whether the number z[0] = zx + i*zy with a constant c = x + i*y
+ belongs to the Julia set. In order to belong, the sequence
+ z[i + 1] = z[i]**2 + c, must not diverge after 'threshold' number of steps.
+ The sequence diverges if the absolute value of z[i+1] is greater than 4.
+
+ :param float zx: the x component of z[0]
+ :param float zy: the y component of z[0]
+ :param float cx: the x component of the constant c
+ :param float cy: the y component of the constant c
+ :param int threshold: the number of iterations to considered it converged
+ """
+ # initial conditions
+ z = complex(zx, zy)
+ c = complex(cx, cy)
+
+ for i in range(threshold):
+ z = z**2 + c
+ if abs(z) > 4.: # it diverged
+ return i
+
+ return threshold - 1 # it didn't diverge
+Obviously, the setup is quite similar as the Mandelbrot Set implementation. The maximum number of iterations is
+denoted as threshold. If the magnitude of the sequence is never greater than 4, the number z₀ belongs to
+the Julia Set and vice-versa.
The number c is giving us the freedom to analyze its impact on the convergence of the sequence, given that the +number of maximum iterations is fixed. One interesting range of values for c is for c = r cos α + i × r sin α +such that r=0.7885 and α ∈ [0, 2π].
The best possible way to make this analysis is to create an animated visualization as the number c changes. +This ameliorates our visual perception and +understanding of such abstract phenomena in a captivating manner. To do so, we use the Matplotlib's Animation API, as +demonstrated in the code below:
import numpy as np
+import matplotlib.pyplot as plt
+import matplotlib.animation as animation
+
+x_start, y_start = -2, -2 # an interesting region starts here
+width, height = 4, 4 # for 4 units up and right
+density_per_unit = 200 # how many pixles per unit
+
+# real and imaginary axis
+re = np.linspace(x_start, x_start + width, width * density_per_unit )
+im = np.linspace(y_start, y_start + height, height * density_per_unit)
+
+
+threshold = 20 # max allowed iterations
+frames = 100 # number of frames in the animation
+
+# we represent c as c = r*cos(a) + i*r*sin(a) = r*e^{i*a}
+r = 0.7885
+a = np.linspace(0, 2*np.pi, frames)
+
+fig = plt.figure(figsize=(10, 10)) # instantiate a figure to draw
+ax = plt.axes() # create an axes object
+
+def animate(i):
+ ax.clear() # clear axes object
+ ax.set_xticks([], []) # clear x-axis ticks
+ ax.set_yticks([], []) # clear y-axis ticks
+
+ X = np.empty((len(re), len(im))) # the initial array-like image
+ cx, cy = r * np.cos(a[i]), r * np.sin(a[i]) # the initial c number
+
+ # iterations for the given threshold
+ for i in range(len(re)):
+ for j in range(len(im)):
+ X[i, j] = julia_quadratic(re[i], im[j], cx, cy, threshold)
+
+ img = ax.imshow(X.T, interpolation="bicubic", cmap='magma')
+ return [img]
+
+anim = animation.FuncAnimation(fig, animate, frames=frames, interval=50, blit=True)
+anim.save('julia_set.gif', writer='imagemagick')
+The logic in the animate function is very similar to the previous example. We update the number c as a function
+of the frame number. Based on that we estimate the convergence of all complex numbers in the defined lattice, given the
+fixed threshold of allowed iterations. Same as before, we save the results in an initially empty matrix X and
+associate them to a color relative to the maximum number of iterations. The resulting animation is illustrated below:
The fractals are really mind-gobbling structures as we saw during this blog. First, we gave a general intuition +of the fractal geometry. Then, we observed two types of fractals: the Mandelbrot and Julia sets. We implemented +them in Python and made interesting animated visualizations of their properties.
Posted +
The ocean is a key component of the Earth climate system. It thus needs a continuous real-time monitoring to help scientists better understand its dynamic and predict its evolution. All around the world, oceanographers have managed to join their efforts and set up a Global Ocean Observing System among which Argo is a key component. Argo is a global network of nearly 4000 autonomous probes or floats measuring pressure, temperature and salinity from the surface to 2000m depth every 10 days. The localisation of these floats is nearly random between the 60th parallels (see live coverage here). All data are collected by satellite in real-time, processed by several data centers and finally merged in a single dataset (collecting more than 2 millions of vertical profiles data) made freely available to anyone.
In this particular case, we want to plot temperature (surface and 1000m deep) data measured by those floats, for the period 2010-2020 and for the Mediterranean sea. We want this plot to be circular and animated, now you start to get the title of this post: Animated polar plot.
First we need some data to work with. To retrieve our temperature values from Argo, we use Argopy, which is a Python library that aims to ease Argo data access, manipulation and visualization for standard users, as well as Argo experts and operators. Argopy returns xarray dataset objects, which make our analysis much easier.
import pandas as pd
+import numpy as np
+from argopy import DataFetcher as ArgoDataFetcher
+argo_loader = ArgoDataFetcher(cache=True)
+#
+# Query surface and 1000m temp in Med sea with argopy
+df1 = argo_loader.region([-1.2,29.,28.,46.,0,10.,'2009-12','2020-01']).to_xarray()
+df2 = argo_loader.region([-1.2,29.,28.,46.,975.,1025.,'2009-12','2020-01']).to_xarray()
+#
+Here we create some arrays we'll use for plotting, we set up a date array and extract day of the year and year itself that will be usefull. Then to build our temperature array, we use xarray very usefull methods : where() and mean(). Then we build a pandas Dataframe, because it's prettier!
# Weekly date array
+daterange=np.arange('2010-01-01','2020-01-03',dtype='datetime64[7D]')
+dayoftheyear=pd.DatetimeIndex(np.array(daterange,dtype='datetime64[D]')+3).dayofyear # middle of the week
+activeyear=pd.DatetimeIndex(np.array(daterange,dtype='datetime64[D]')+3).year # extract year
+
+# Init final arrays
+tsurf=np.zeros(len(daterange))
+t1000=np.zeros(len(daterange))
+
+# Filling arrays
+for i in range(len(daterange)):
+ i1=(df1['TIME']>=daterange[i])&(df1['TIME']<daterange[i]+7)
+ i2=(df2['TIME']>=daterange[i])&(df2['TIME']<daterange[i]+7)
+ tsurf[i]=df1.where(i1,drop=True)['TEMP'].mean().values
+ t1000[i]=df2.where(i2,drop=True)['TEMP'].mean().values
+
+# Creating dataframe
+d = {'date': np.array(daterange,dtype='datetime64[D]'), 'tsurf': tsurf, 't1000': t1000}
+ndf = pd.DataFrame(data=d)
+ndf.head()
+
+ date tsurf t1000
+0 2009-12-31 15.725000 13.306133
+1 2010-01-07 15.530414 13.315658
+2 2010-01-14 15.307378 13.300347
+3 2010-01-21 14.954195 13.300647
+4 2010-01-28 14.708816 13.300274
+Then it's time to plot, for that we first need to import what we need, and set some usefull variables.
import matplotlib.pyplot as plt
+import matplotlib
+plt.rcParams['xtick.major.pad']='17'
+plt.rcParams["axes.axisbelow"] = False
+matplotlib.rc('axes',edgecolor='w')
+from matplotlib.lines import Line2D
+from matplotlib.animation import FuncAnimation
+from IPython.display import HTML
+
+big_angle= 360/12 # How we split our polar space
+date_angle=((360/365)*dayoftheyear)*np.pi/180 # For a day, a corresponding angle
+# inner and outer ring limit values
+inner=10
+outer=30
+# setting our color values
+ocean_color = ["#ff7f50","#004752"]
+Now we want to make our axes like we want, for that we build a function dress_axes that will be called during the animation process. Here we plot some bars with an offset (combination of bottom and ylim after). Those bars are actually our background, and the offset allows us to plot a legend in the middle of the plot.
def dress_axes(ax):
+ ax.set_facecolor('w')
+ ax.set_theta_zero_location("N")
+ ax.set_theta_direction(-1)
+ # Here is how we position the months labels
+ middles=np.arange(big_angle/2 ,360, big_angle)*np.pi/180
+ ax.set_xticks(middles)
+ ax.set_xticklabels(['January', 'February', 'March', 'April', 'May', 'June', 'July', 'August','September','October','November','December'])
+ ax.set_yticks([15,20,25])
+ ax.set_yticklabels(['15°C','20°C','25°C'])
+ # Changing radial ticks angle
+ ax.set_rlabel_position(359)
+ ax.tick_params(axis='both',color='w')
+ plt.grid(None,axis='x')
+ plt.grid(axis='y',color='w', linestyle=':', linewidth=1)
+ # Here is the bar plot that we use as background
+ bars = ax.bar(middles, outer, width=big_angle*np.pi/180, bottom=inner, color='lightgray', edgecolor='w',zorder=0)
+ plt.ylim([2,outer])
+ # Custom legend
+ legend_elements = [Line2D([0], [0], marker='o', color='w', label='Surface', markerfacecolor=ocean_color[0], markersize=15),
+ Line2D([0], [0], marker='o', color='w', label='1000m', markerfacecolor=ocean_color[1], markersize=15),
+ ]
+ ax.legend(handles=legend_elements, loc='center', fontsize=13, frameon=False)
+ # Main title for the figure
+ plt.suptitle('Mediterranean temperature from Argo profiles',fontsize=16,horizontalalignment='center')
+From there we can plot the frame of our plot.
fig = plt.figure(figsize=(10,10))
+ax = fig.add_subplot(111, polar=True)
+dress_axes(ax)
+plt.show()
+
Then it's finally time to plot our data. Since we want to animated the plot, we'll build a function that will be called in FuncAnimation later on. Since the state of the plot changes on every time stamp, we have to redress the axes for each frame, easy with our dress_axes function. Then we plot our temperature data using basic plot(): thin lines for historical measurements, thicker lines for the current year.
def draw_data(i):
+ # Clear
+ ax.cla()
+ # Redressing axes
+ dress_axes(ax)
+ # Limit between thin lines and thick line, this is current date minus 51 weeks basically.
+ # why 51 and not 52 ? That create a small gap before the current date, which is prettier
+ i0=np.max([i-51,0])
+
+ ax.plot(date_angle[i0:i+1], ndf['tsurf'][i0:i+1],'-',color=ocean_color[0],alpha=1.0,linewidth=5)
+ ax.plot(date_angle[0:i+1], ndf['tsurf'][0:i+1],'-',color=ocean_color[0],linewidth=0.7)
+
+ ax.plot(date_angle[i0:i+1], ndf['t1000'][i0:i+1],'-',color=ocean_color[1],alpha=1.0,linewidth=5)
+ ax.plot(date_angle[0:i+1], ndf['t1000'][0:i+1],'-',color=ocean_color[1],linewidth=0.7)
+
+ # Plotting a line to spot the current date easily
+ ax.plot([date_angle[i],date_angle[i]],[inner,outer],'k-',linewidth=0.5)
+ # Display the current year as a title, just beneath the suptitle
+ plt.title(str(activeyear[i]),fontsize=16,horizontalalignment='center')
+
+# Test it
+draw_data(322)
+plt.show()
+
Finally it's time to animate, using FuncAnimation. Then we save it as a mp4 file or we display it in our notebook with HTML(anim.to_html5_video()).
anim = FuncAnimation(fig, draw_data, interval=40, frames=len(daterange)-1, repeat=False)
+#anim.save('ArgopyUseCase_MedTempAnimation.mp4')
+HTML(anim.to_html5_video())
+
Posted +
It's my great pleasure to announce that I've finished my book on matplotlib and it is now freely available at www.labri.fr/perso/nrougier/scientific-visualization.html while sources for the book are hosted at github.com/rougier/scientific-visualization-book.
The Python scientific visualisation landscape is huge. It is composed of a myriad of tools, ranging from the most versatile and widely used down to the more specialised and confidential. Some of these tools are community based while others are developed by companies. Some are made specifically for the web, others are for the desktop only, some deal with 3D and large data, while others target flawless 2D rendering. In this landscape, Matplotlib has a very special place. It is a versatile and powerful library that allows you to design very high quality figures, suitable for scientific publishing. It also offers a simple and intuitive interface as well as an object oriented architecture that allows you to tweak anything within a figure. Finally, it can be used as a regular graphic library in order to design non‐scientific figures. This book is organized into four parts. The first part considers the fundamental principles of the Matplotlib library. This includes reviewing the different parts that constitute a figure, the different coordinate systems, the available scales and projections, and we’ll also introduce a few concepts related to typography and colors. The second part is dedicated to the actual design of a figure. After introducing some simple rules for generating better figures, we’ll then go on to explain the Matplotlib defaults and styling system before diving on into figure layout organization. We’ll then explore the different types of plot available and see how a figure can be ornamented with different elements. The third part is dedicated to more advanced concepts, namely 3D figures, optimization & animation. The fourth and final part is a collection of showcases.
Posted +
Code-switching is the practice of alternating between two or more languages in the context of a single conversation, either consciously or unconsciously. As someone who grew up bilingual and is currently learning other languages, I find code-switching a fascinating facet of communication from not only a purely linguistic perspective, but also a social one. In particular, I've personally found that code-switching often helps build a sense of community and familiarity in a group and that the unique ways in which speakers code-switch with each other greatly contribute to shaping group dynamics.
This is something that's evident in seven-member pop boy group WayV. Aside from their discography, artistry, and group chemistry, WayV is well-known among fans and many non-fans alike for their multilingualism and code-switching, which many fans have affectionately coined as “WayV language.” Every member in the group is fluent in both Mandarin and Korean, and at least one member in the group is fluent in one or more of the following: English, Cantonese, Thai, Wenzhounese, and German. It's an impressive trait that's become a trademark of WayV as they've quickly drawn a global audience since their debut in January 2019. Their multilingualism is reflected in their music as well. On top of their regular album releases in Mandarin, WayV has also released singles in Korean and English, with their latest single “Bad Alive (English Ver.)” being a mix of English, Korean, and Mandarin.
As an independent translator who translates WayV content into English, I've become keenly aware of the true extent and rate of WayV's code-switching when communicating with each other. In a lot of their content, WayV frequently switches between three or more languages every couple of seconds, a phenomenon that can make translating quite challenging at times, but also extremely rewarding and fun. I wanted to be able to present this aspect of WayV in a way that would both highlight their linguistic skills and present this dimension of their group dynamic in a more concrete, quantitative, and visually intuitive manner, beyond just stating that “they code-switch a lot.” This prompted me to make step charts - perfect for displaying data that changes at irregular intervals but remains constant between the changes - in hopes of enriching the viewer's experience and helping make a potentially abstract concept more understandable and readily consumable. With a step chart, it becomes more apparent to the viewer the extent of how a group communicates, and cross-sections of the graph allow a rudimentary look into how multilinguals influence each other in code-switching.
This tutorial on creating step charts uses one of WayV's livestreams as an example. There were four members in this livestream and a total of eight languages/dialects spoken. I will go through the basic steps of creating a step chart that depicts the frequency of code-switching for just one member. A full code chunk that shows how to layer two or more step chart lines in one graph to depict code-switching for multiple members can be found near the end.
First, we import the required libraries and load the data into a Pandas dataframe.
import pandas as pd
+import matplotlib.pyplot as plt
+import seaborn as sns
+This dataset includes the timestamp of every switch (in seconds) and the language of switch for one speaker.
df_h = pd.read_csv("WayVHendery.csv")
+HENDERY = df_h.reset_index()
+HENDERY.head()
+| index | time | lang |
|---|---|---|
| 0 | 2 | ENG |
| 1 | 3 | KOR |
| 2 | 10 | ENG |
| 3 | 13 | MAND |
| 4 | 15 | ENG |
With the dataset loaded, we can now set up our graph in terms of determining the size of the figure, dpi, font size, and axes limits. We can also play around with the aesthetics, such as modifying the colors of our plot. These few simple steps easily transform the default all-white graph into a more visually appealing one.
fig, ax = plt.subplots(figsize = (20,12))
+
sns.set(rc={'axes.facecolor':'aliceblue', 'figure.facecolor':'c'})
+fig, ax = plt.subplots(figsize = (20,12), dpi = 300)
+
+plt.xlabel("Duration of Instagram Live (seconds)", fontsize = 18)
+plt.ylabel("Cumulative Number of Times of Code-Switching", fontsize = 18)
+
+plt.xlim(0, 570)
+plt.ylim(0, 85)
+
Following this, we can make our step chart line easily with matplotlib.pyplot.step, in which we plot the x and y values and determine the text of the legend, color of the step chart line, and width of the step chart line.
ax.step(HENDERY.time, HENDERY.index, label = "HENDERY", color = "palevioletred", linewidth = 4)
+
Of course, we want to know not only how many switches there were and when they occurred, but also to what language the member switched. For this, we can write a for loop that labels each switch with its respective language as recorded in our dataset.
for x,y,z in zip(HENDERY["time"], HENDERY["index"], HENDERY["lang"]):
+ label = z
+ ax.annotate(label, #text
+ (x,y), #label coordinate
+ textcoords = "offset points", #how to position text
+ xytext = (15,-5), #distance from text to coordinate (x,y)
+ ha = "center", #alignment
+ fontsize = 8.5) #font size of text
+
Now add a title, save the graph, and there you have it!
plt.title("WayV Livestream Code-Switching", fontsize = 35)
+
+fig.savefig("wayv_codeswitching.png", bbox_inches = "tight", facecolor = fig.get_facecolor())
+Below is the complete code for layering step chart lines for multiple speakers in one graph. You can see how easy it is to take the code for visualizing the code-switching of one speaker and adapt it to visualizing that of multiple speakers. In addition, you can see that I've intentionally left the title blank so I can incorporate external graphic adjustments after I created the chart in Matplotlib, such as the addition of my social media handle and the use of a specific font I wanted, which you can see in the final graph. With visualizations being all about communicating information, I believe using Matplotlib in conjunction with simple elements of graphic design can be another way to make whatever you're presenting that little bit more effective and personal, especially when you're doing so on social media platforms.
# Initialize graph color and size
+sns.set(rc={'axes.facecolor':'aliceblue', 'figure.facecolor':'c'})
+
+fig, ax = plt.subplots(figsize = (20,12), dpi = 120)
+
+# Set up axes and labels
+plt.xlabel("Duration of Instagram Live (seconds)", fontsize = 18)
+plt.ylabel("Cumulative Number of Times of Code-Switching", fontsize = 18)
+
+plt.xlim(0, 570)
+plt.ylim(0, 85)
+
+# Layer step charts for each speaker
+ax.step(YANGYANG.time, YANGYANG.index, label = "YANGYANG", color = "firebrick", linewidth = 4)
+ax.step(HENDERY.time, HENDERY.index, label = "HENDERY", color = "palevioletred", linewidth = 4)
+ax.step(TEN.time, TEN.index, label = "TEN", color = "mediumpurple", linewidth = 4)
+ax.step(KUN.time, KUN.index, label = "KUN", color = "mediumblue", linewidth = 4)
+
+# Add legend
+ax.legend(fontsize = 17)
+
+# Label each data point with the language switch
+for i in (KUN, TEN, HENDERY, YANGYANG): #for each dataset
+ for x,y,z in zip(i["time"], i["index"], i["lang"]): #looping within the dataset
+ label = z
+ ax.annotate(label, #text
+ (x,y), #label coordinate
+ textcoords = "offset points", #how to position text
+ xytext = (15,-5), #distance from text to coordinate (x,y)
+ ha = "center", #alignment
+ fontsize = 8.5) #font size of text
+
+# Add title (blank to leave room for external graphics)
+plt.title("\n\n", fontsize = 35)
+
+# Save figure
+fig.savefig("wayv_codeswitching.png", bbox_inches = "tight", facecolor = fig.get_facecolor())
+
+Languages/dialects: Korean (KOR), English (ENG), Mandarin (MAND), German (GER), Cantonese (CANT), Hokkien (HOKK), Teochew (TEO), Thai (THAI)
186 total switches! That's approximately one code-switch in the group every 2.95 seconds.
And voilà! There you have it: a brief guide on how to make step charts. While I utilized step charts here to visualize code-switching, you can use them to visualize whatever data you would like. Please feel free to contact me here if you have any questions or comments. I hope you enjoyed this tutorial, and thank you so much for reading!
Posted +
My name is Ted Petrou, founder of Dunder Data, and in this tutorial you will learn how to create the new Tesla Cybertruck using Matplotlib. I was inspired by the image below which was originally created by Lynn Fisher (without Matplotlib).
Before going into detail, let's jump to the results. Here is the completed recreation of the Tesla Cybertruck that drives off the screen.
A tutorial now follows containing all the steps that creates a Tesla Cybertruck that drives. It covers the following topics:
Understanding these topics should give you enough to start animating your own figures in Matplotlib. This tutorial is not suited for those with no Matplotlib experience. You need to understand the relationship between the Figure and Axes and how to use the object-oriented interface of Matplotlib.
We first create a Matplotlib Figure without any Axes (the plotting surface). The function create_axes adds an Axes to the Figure, sets the x-limits to be twice the y-limits (to match the ratio of the figure dimensions (16 x 8)), fills in the background with two different dark colors using fill_between, and adds grid lines to make it easier to plot the objects in the exact place you desire. Set the draft parameter to False when you want to remove the grid lines, tick marks, and tick labels.
import numpy as np
+import matplotlib.pyplot as plt
+%matplotlib inline
+
+fig = plt.Figure(figsize=(16, 8))
+
+def create_axes(draft=True):
+ ax = fig.add_subplot()
+ ax.grid(True)
+ ax.set_ylim(0, 1)
+ ax.set_xlim(0, 2)
+ ax.fill_between(x=[0, 2], y1=.36, y2=1, color='black')
+ ax.fill_between(x=[0, 2], y1=0, y2=.36, color='#101115')
+ if not draft:
+ ax.grid(False)
+ ax.axis('off')
+
+create_axes()
+fig
+
Most of the Cybertruck is composed of shapes (patches in Matplotlib terminology) - circles, rectangles, and polygons. These shapes are available in the patches Matplotlib module. After importing, we instantiate single instances of these patches and then call the add_patch method to add the patch to the Axes.
For the Cybertruck, I used three patches, Polygon, Rectangle, and Circle. They each have different parameters available in their constructor. I first constructed the body of the car as four polygons. Two other polygons were used for the rims. Each polygon is provided a list of x, y coordinates where the corner points are located. Matplotlib connects all the points in the order given and fills it in with the provided color.
Notice how the Axes is retrieved as the first line of the function. This is used throughout the tutorial.
from matplotlib.patches import Polygon, Rectangle, Circle
+
+def create_body():
+ ax = fig.axes[0]
+ top = Polygon([[.62, .51], [1, .66], [1.6, .56]], color='#DCDCDC')
+ windows = Polygon([[.74, .54], [1, .64], [1.26, .6], [1.262, .57]], color='black')
+ windows_bottom = Polygon([[.8, .56], [1, .635], [1.255, .597],
+ [1.255, .585]], color='#474747')
+ base = Polygon([[.62, .51], [.62, .445], [.67, .5], [.78, .5], [.84, .42],
+ [1.3, .423], [1.36, .51], [1.44, .51], [1.52, .43], [1.58, .44],
+ [1.6, .56]], color="#1E2329")
+ left_rim = Polygon([[.62, .445], [.67, .5], [.78, .5], [.84, .42],
+ [.824, .42], [.77, .49],[.674, .49], [.633, .445]], color='#373E48')
+ right_rim = Polygon([[1.3, .423], [1.36, .51], [1.44, .51], [1.52, .43],
+ [1.504, .43], [1.436, .498], [1.364, .498],
+ [1.312, .423]], color='#4D586A')
+ ax.add_patch(top)
+ ax.add_patch(windows)
+ ax.add_patch(windows_bottom)
+ ax.add_patch(base)
+ ax.add_patch(left_rim)
+ ax.add_patch(right_rim)
+
+create_body()
+fig
+
I used three Circle patches for each of the tires. You must provide the center and radius. For the innermost circles (the “spokes”), I've set the zorder to 99. The zorder determines the order of how plotting objects are layered on top of each other. The higher the number, the higher up on the stack of layers the object will be plotted. During the next step, we will draw some rectangles through the tires and they need to be plotted underneath these spokes.
def create_tires():
+ ax = fig.axes[0]
+ left_tire = Circle((.724, .39), radius=.075, color="#202328")
+ right_tire = Circle((1.404, .39), radius=.075, color="#202328")
+ left_inner_tire = Circle((.724, .39), radius=.052, color="#15191C")
+ right_inner_tire = Circle((1.404, .39), radius=.052, color="#15191C")
+ left_spoke = Circle((.724, .39), radius=.019, color="#202328", zorder=99)
+ right_spoke = Circle((1.404, .39), radius=.019, color="#202328", zorder=99)
+ left_inner_spoke = Circle((.724, .39), radius=.011, color="#131418", zorder=99)
+ right_inner_spoke = Circle((1.404, .39), radius=.011, color="#131418", zorder=99)
+
+ ax.add_patch(left_tire)
+ ax.add_patch(right_tire)
+ ax.add_patch(left_inner_tire)
+ ax.add_patch(right_inner_tire)
+ ax.add_patch(left_spoke)
+ ax.add_patch(right_spoke)
+ ax.add_patch(left_inner_spoke)
+ ax.add_patch(right_inner_spoke)
+
+create_tires()
+fig
+
I used the Rectangle patch to represent the two ‘axles’ (this isn't the correct term, but you'll see what I mean) going through the tires. You must provide a coordinate for the lower left corner, a width, and a height. You can also provide it an angle (in degrees) to control its orientation. Notice that they go under the spokes plotted from above. This is due to their lower zorder.
def create_axles():
+ ax = fig.axes[0]
+ left_left_axle = Rectangle((.687, .427), width=.104, height=.005, angle=315, color='#202328')
+ left_right_axle = Rectangle((.761, .427), width=.104, height=.005, angle=225, color='#202328')
+ right_left_axle = Rectangle((1.367, .427), width=.104, height=.005, angle=315, color='#202328')
+ right_right_axle = Rectangle((1.441, .427), width=.104, height=.005, angle=225, color='#202328')
+
+ ax.add_patch(left_left_axle)
+ ax.add_patch(left_right_axle)
+ ax.add_patch(right_left_axle)
+ ax.add_patch(right_right_axle)
+
+create_axles()
+fig
+
The front bumper, head light, tail light, door and window lines are added below. I used regular Matplotlib lines for some of these. Those lines are not patches and get added directly to the Axes without any other additional method.
def create_other_details():
+ ax = fig.axes[0]
+ # other details
+ front = Polygon([[.62, .51], [.597, .51], [.589, .5], [.589, .445], [.62, .445]], color='#26272d')
+ front_bottom = Polygon([[.62, .438], [.58, .438], [.58, .423], [.62, .423]], color='#26272d')
+ head_light = Polygon([[.62, .51], [.597, .51], [.589, .5], [.589, .5], [.62, .5]], color='aqua')
+ step = Polygon([[.84, .39], [.84, .394], [1.3, .397], [1.3, .393]], color='#1E2329')
+
+ # doors
+ ax.plot([.84, .84], [.42, .523], color='black', lw=.5)
+ ax.plot([1.02, 1.04], [.42, .53], color='black', lw=.5)
+ ax.plot([1.26, 1.26], [.42, .54], color='black', lw=.5)
+ ax.plot([.84, .85], [.523, .547], color='black', lw=.5)
+ ax.plot([1.04, 1.04], [.53, .557], color='black', lw=.5)
+ ax.plot([1.26, 1.26], [.54, .57], color='black', lw=.5)
+
+ # window lines
+ ax.plot([.87, .88], [.56, .59], color='black', lw=1)
+ ax.plot([1.03, 1.04], [.56, .63], color='black', lw=.5)
+
+ # tail light
+ tail_light = Circle((1.6, .56), radius=.007, color='red', alpha=.6)
+ tail_light_center = Circle((1.6, .56), radius=.003, color='yellow', alpha=.6)
+ tail_light_up = Polygon([[1.597, .56], [1.6, .6], [1.603, .56]], color='red', alpha=.4)
+ tail_light_right = Polygon([[1.6, .563], [1.64, .56], [1.6, .557]], color='red', alpha=.4)
+ tail_light_down = Polygon([[1.597, .56], [1.6, .52], [1.603, .56]], color='red', alpha=.4)
+
+ ax.add_patch(front)
+ ax.add_patch(front_bottom)
+ ax.add_patch(head_light)
+ ax.add_patch(step)
+ ax.add_patch(tail_light)
+ ax.add_patch(tail_light_center)
+ ax.add_patch(tail_light_up)
+ ax.add_patch(tail_light_right)
+ ax.add_patch(tail_light_down)
+
+create_other_details()
+fig
+
The head light beam has a distinct color gradient that dissipates into the night sky. This is challenging to complete. I found an excellent answer on Stack Overflow from user Joe Kington on how to do this. We begin by using the imshow function which creates images from 3-dimensional arrays. Our image will simply be a rectangle of colors.
We create a 1 x 100 x 4 array that represents 1 row by 100 columns of points of RGBA (red, green, blue, alpha) values. Every point is given the same red, green, and blue values of (0, 1, 1) which represents the color ‘aqua’. The alpha value represents opacity and ranges between 0 and 1 with 0 being completely transparent (invisible) and 1 being opaque. We would like the opacity to decrease as the light extends further from the head light (that is further to the left). The NumPy linspace function is used to create an array of 100 numbers increasing linearly from 0 to 1. This array will be set as the alpha values.
The extent parameter defines the rectangular region where the image will be shown. The four values correspond to xmin, xmax, ymin, and ymax. The 100 alpha values will be mapped to this region beginning from the left. The array of alphas begins at 0, which means that the very left of this rectangular region will be transparent. The opacity will increase moving to the right-side of the rectangle where it eventually reaches 1.
import matplotlib.colors as mcolors
+
+def create_headlight_beam():
+ ax = fig.axes[0]
+ z = np.empty((1, 100, 4), dtype=float)
+ rgb = mcolors.colorConverter.to_rgb('aqua')
+ alphas = np.linspace(0, 1, 100)
+ z[:, :, :3] = rgb
+ z[:, :, -1] = alphas
+ im = ax.imshow(z, extent=[.3, .589, .501, .505], zorder=1)
+
+create_headlight_beam()
+fig
+
The cloud of points surrounding the headlight beam is even more challenging to complete. This time, a 100 x 100 grid of points was used to control the opacity. The opacity is directly proportional to the vertical distance from the center beam. Additionally, if a point was outside of the diagonal of the rectangle defined by extent, its opacity was set to 0.
def create_headlight_cloud():
+ ax = fig.axes[0]
+ z2 = np.empty((100, 100, 4), dtype=float)
+ rgb = mcolors.colorConverter.to_rgb('aqua')
+ z2[:, :, :3] = rgb
+ for j, x in enumerate(np.linspace(0, 1, 100)):
+ for i, y in enumerate(np.abs(np.linspace(-.2, .2, 100))):
+ if x * .2 > y:
+ z2[i, j, -1] = 1 - (y + .8) ** 2
+ else:
+ z2[i, j, -1] = 0
+ im2 = ax.imshow(z2, extent=[.3, .65, .45, .55], zorder=1)
+
+create_headlight_cloud()
+fig
+
All of our work from above can be placed in a single function that draws the car. This will be used when initializing our animation. Notice, that the first line of the function clears the Figure, which removes our Axes. If we don't clear the Figure, then we will keep adding more and more Axes each time this function is called. Since this is our final product, we set draft to False.
def draw_car():
+ fig.clear()
+ create_axes(draft=False)
+ create_body()
+ create_tires()
+ create_axles()
+ create_other_details()
+ create_headlight_beam()
+ create_headlight_beam()
+
+draw_car()
+fig
+
Animation in Matplotlib is fairly straightforward. You must create a function that updates the position of the objects in your figure for each frame. This function is called repeatedly for each frame.
In the update function below, we loop through each patch, line, and image in our Axes and reduce the x-value of each plotted object by .015. This has the effect of moving the truck to the left. The trickiest part was changing the x and y values for the rectangular tire ‘axles’ so that it appeared that the tires were rotating. Some basic trigonometry helps calculate this.
Implicitly, Matplotlib passes the update function the frame number as an integer as the first argument. We accept this input as the parameter frame_number. We only use it in one place, and that is to do nothing during the first frame.
Finally, the FuncAnimation class from the animation module is used to construct the animation. We provide it our original Figure, the function to update the Figure (update), a function to initialize the Figure (draw_car), the total number of frames, and any extra arguments used during update (fargs).
from matplotlib.animation import FuncAnimation
+
+def update(frame_number, x_delta, radius, angle):
+ if frame_number == 0:
+ return
+ ax = fig.axes[0]
+ for patch in ax.patches:
+ if isinstance(patch, Polygon):
+ arr = patch.get_xy()
+ arr[:, 0] -= x_delta
+ elif isinstance(patch, Circle):
+ x, y = patch.get_center()
+ patch.set_center((x - x_delta, y))
+ elif isinstance(patch, Rectangle):
+ xd_old = -np.cos(np.pi * patch.angle / 180) * radius
+ yd_old = -np.sin(np.pi * patch.angle / 180) * radius
+ patch.angle += angle
+ xd = -np.cos(np.pi * patch.angle / 180) * radius
+ yd = -np.sin(np.pi * patch.angle / 180) * radius
+ x = patch.get_x()
+ y = patch.get_y()
+ x_new = x - x_delta + xd - xd_old
+ y_new = y + yd - yd_old
+ patch.set_x(x_new)
+ patch.set_y(y_new)
+
+ for line in ax.lines:
+ xdata = line.get_xdata()
+ line.set_xdata(xdata - x_delta)
+
+ for image in ax.images:
+ extent = image.get_extent()
+ extent[0] -= x_delta
+ extent[1] -= x_delta
+
+animation = FuncAnimation(fig, update, init_func=draw_car, frames=110,
+ repeat=False, fargs=(.015, .052, 4))
+Finally, we can save the animation as an mp4 file (you must have ffmpeg installed for this to work). We set the frames-per-second (fps) to 30. From above, the total number of frames is 110 (enough to move the truck off the screen) so the video will last nearly four seconds (110 / 30).
animation.save('tesla_animate.mp4', fps=30, bitrate=3000)
+I encourage you to add more components to your Cybertruck animation to personalize the creation. I suggest encapsulating each addition with a function as done in this tutorial.
Posted +
This post will outline how we can leverage gridspec to create ridgeplots in Matplotlib. While this is a relatively straightforward tutorial, some experience working with sklearn would be beneficial. Naturally it being a vast undertaking, this will not be an sklearn tutorial, those interested can read through the docs here. However, I will use its KernelDensity module from sklearn.neighbors.
import pandas as pd
+import numpy as np
+from sklearn.neighbors import KernelDensity
+
+import matplotlib as mpl
+import matplotlib.pyplot as plt
+import matplotlib.gridspec as grid_spec
+I'll be using some mock data I created. You can grab the dataset from GitHub here if you want to play along. The data looks at aptitude test scores broken down by country, age, and sex.
data = pd.read_csv("mock-european-test-results.csv")
+| country | age | sex | score |
|---|---|---|---|
| Italy | 21 | female | 0.77 |
| Spain | 20 | female | 0.87 |
| Italy | 24 | female | 0.39 |
| United Kingdom | 20 | female | 0.70 |
| Germany | 20 | male | 0.25 |
| … |
GridSpec is a Matplotlib module that allows us easy creation of subplots. We can control the number of subplots, the positions, the height, width, and spacing between each. As a basic example, let's create a quick template. The key parameters we'll be focusing on are nrows, ncols, and width_ratios.
nrowsand ncols divide our figure into areas we can add axes to. width_ratioscontrols the width of each of our columns. If we create something like GridSpec(2,2,width_ratios=[2,1]), we are subsetting our figure into 2 rows, 2 columns, and setting our width ratio to 2:1, i.e., that the first column will take up two times the width of the figure.
What's great about GridSpec is that now we have created those subsets, we are not bound to them, as we will see below.
Note: I am using my own theme, so plots will look different. Creating custom themes is outside the scope of this tutorial (but I may write one in the future).
gs = (grid_spec.GridSpec(2,2,width_ratios=[2,1]))
+
+fig = plt.figure(figsize=(8,6))
+
+ax = fig.add_subplot(gs[0:1,0])
+ax1 = fig.add_subplot(gs[1:,0])
+ax2 = fig.add_subplot(gs[0:,1:])
+
+ax_objs = [ax,ax1,ax2]
+n = ["",1,2]
+
+i = 0
+for ax_obj in ax_objs:
+ ax_obj.text(0.5,0.5,"ax{}".format(n[i]),
+ ha="center",color="red",
+ fontweight="bold",size=20)
+ i += 1
+
+plt.show()
+
I won't get into more detail about what everything does here. If you are interested in learning more about figures, axes, and gridspec, Akash Palrecha has written a very nice guide here.
We have a couple of options here. The easiest by far is to stick with the pipes built into pandas. All that's needed is to select the column and add plot.kde. This defaults to a Scott bandwidth method, but you can choose a Silverman method, or add your own. Let's use GridSpec again to plot the distribution for each country. First we'll grab the unique country names and create a list of colors.
countries = [x for x in np.unique(data.country)]
+colors = ['#0000ff', '#3300cc', '#660099', '#990066', '#cc0033', '#ff0000']
+Next we'll loop through each country and color to plot our data. Unlike the above we will not explicitly declare how many rows we want to plot. The reason for this is to make our code more dynamic. If we set a specific number of rows and specific number of axes objects, we're creating inefficient code. This is a bit of an aside, but when creating visualizations, you should always aim to reduce and reuse. By reduce, we specifically mean lessening the number of variables we are declaring and the unnecessary code associated with that. We are plotting data for six countries, what happens if we get data for 20 countries? That's a lot of additional code. Related, by not explicitly declaring those variables we make our code adaptable and ready to be scripted to automatically create new plots when new data of the same kind becomes available.
gs = (grid_spec.GridSpec(len(countries),1))
+
+fig = plt.figure(figsize=(8,6))
+
+i = 0
+
+#creating empty list
+ax_objs = []
+
+for country in countries:
+ # creating new axes object and appending to ax_objs
+ ax_objs.append(fig.add_subplot(gs[i:i+1, 0:]))
+
+ # plotting the distribution
+ plot = (data[data.country == country]
+ .score.plot.kde(ax=ax_objs[-1],color="#f0f0f0", lw=0.5)
+ )
+
+ # grabbing x and y data from the kde plot
+ x = plot.get_children()[0]._x
+ y = plot.get_children()[0]._y
+
+ # filling the space beneath the distribution
+ ax_objs[-1].fill_between(x,y,color=colors[i])
+
+ # setting uniform x and y lims
+ ax_objs[-1].set_xlim(0, 1)
+ ax_objs[-1].set_ylim(0,2.2)
+
+ i += 1
+
+plt.tight_layout()
+plt.show()
+
We're not quite at ridge plots yet, but let's look at what's going on here. You'll notice instead of setting an explicit number of rows, we've set it to the length of our countries list - gs = (grid_spec.GridSpec(len(countries),1)). This gives us flexibility for future plotting with the ability to plot more or less countries without needing to adjust the code.
Just after the for loop we create each axes object: ax_objs.append(fig.add_subplot(gs[i:i+1, 0:])). Before the loop we declared i = 0. Here we are saying create axes object from row 0 to 1, the next time the loop runs it creates an axes object from row 1 to 2, then 2 to 3, 3 to 4, and so on.
Following this we can use ax_objs[-1] to access the last created axes object to use as our plotting area.
Next, we create the kde plot. We declare this as a variable so we can retrieve the x and y values to use in the fill_between that follows.
Once again using GridSpec, we can adjust the spacing between each of the subplots. We can do this by adding one line outside of the loop before plt.tight_layout()The exact value will depend on your distribution so feel free to play around with the exact value:
gs.update(hspace= -0.5)
+
Now our axes objects are overlapping! Great-ish. Each axes object is hiding the one layered below it. We could just add ax_objs[-1].axis("off") to our for loop, but if we do that we will lose our xticklabels. Instead we will create a variable to access the background of each axes object, and we will loop through each line of the border (spine) to turn them off. As we only need the xticklabels for the final plot, we will add an if statement to handle that. We will also add in our country labels here. In our for loop we add:
# make background transparent
+rect = ax_objs[-1].patch
+rect.set_alpha(0)
+
+# remove borders, axis ticks, and labels
+ax_objs[-1].set_yticklabels([])
+ax_objs[-1].set_ylabel('')
+
+if i == len(countries)-1:
+ pass
+else:
+ ax_objs[-1].set_xticklabels([])
+
+spines = ["top","right","left","bottom"]
+for s in spines:
+ ax_objs[-1].spines[s].set_visible(False)
+
+country = country.replace(" ","\n")
+ax_objs[-1].text(-0.02,0,country,fontweight="bold",fontsize=14,ha="center")
+
+
As an alternative to the above, we can use the KernelDensity module from sklearn.neighbors to create our distribution. This gives us a bit more control over our bandwidth. The method here is taken from Jake VanderPlas's fantastic Python Data Science Handbook, you can read his full excerpt here. We can reuse most of the above code, but need to make a couple of changes. Rather than repeat myself, I'll add the full snippet here and you can see the changes and minor additions (added title, label to xaxis).
countries = [x for x in np.unique(data.country)]
+colors = ['#0000ff', '#3300cc', '#660099', '#990066', '#cc0033', '#ff0000']
+
+gs = grid_spec.GridSpec(len(countries),1)
+fig = plt.figure(figsize=(16,9))
+
+i = 0
+
+ax_objs = []
+for country in countries:
+ country = countries[i]
+ x = np.array(data[data.country == country].score)
+ x_d = np.linspace(0,1, 1000)
+
+ kde = KernelDensity(bandwidth=0.03, kernel='gaussian')
+ kde.fit(x[:, None])
+
+ logprob = kde.score_samples(x_d[:, None])
+
+ # creating new axes object
+ ax_objs.append(fig.add_subplot(gs[i:i+1, 0:]))
+
+ # plotting the distribution
+ ax_objs[-1].plot(x_d, np.exp(logprob),color="#f0f0f0",lw=1)
+ ax_objs[-1].fill_between(x_d, np.exp(logprob), alpha=1,color=colors[i])
+
+
+ # setting uniform x and y lims
+ ax_objs[-1].set_xlim(0,1)
+ ax_objs[-1].set_ylim(0,2.5)
+
+ # make background transparent
+ rect = ax_objs[-1].patch
+ rect.set_alpha(0)
+
+ # remove borders, axis ticks, and labels
+ ax_objs[-1].set_yticklabels([])
+
+ if i == len(countries)-1:
+ ax_objs[-1].set_xlabel("Test Score", fontsize=16,fontweight="bold")
+ else:
+ ax_objs[-1].set_xticklabels([])
+
+ spines = ["top","right","left","bottom"]
+ for s in spines:
+ ax_objs[-1].spines[s].set_visible(False)
+
+ adj_country = country.replace(" ","\n")
+ ax_objs[-1].text(-0.02,0,adj_country,fontweight="bold",fontsize=14,ha="right")
+
+
+ i += 1
+
+gs.update(hspace=-0.7)
+
+fig.text(0.07,0.85,"Distribution of Aptitude Test Results from 18 – 24 year-olds",fontsize=20)
+
+plt.tight_layout()
+plt.show()
+
I'll finish this off with a little project to put the above code into practice. The data provided also contains information on whether the test taker was male or female. Using the above code as a template, see how you get on creating something like this:
For those more ambitious, this could be turned into a split violin plot with males on one side and females on the other. Is there a way to combine the ridge and violin plot?
I'd love to see what people come back with so if you do create something, send it to me on twitter here!
Posted +
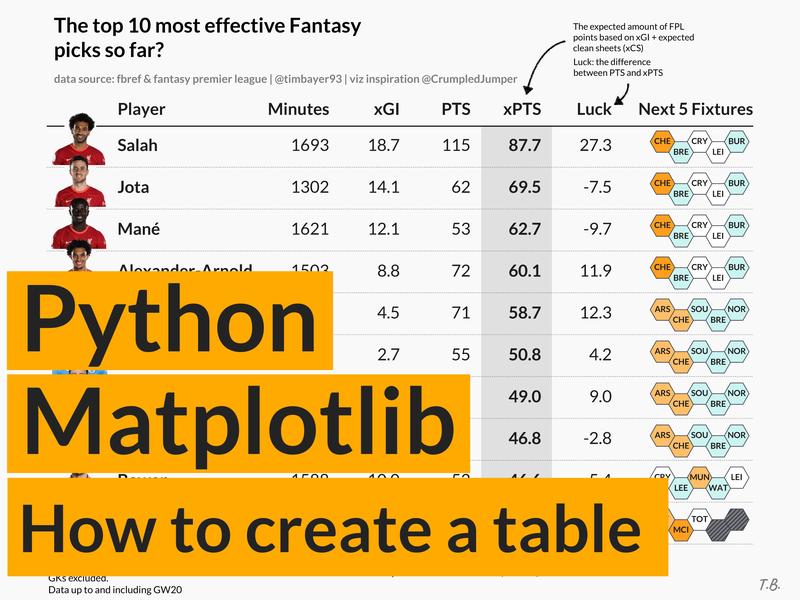
Matplotlib has a really nice 3D +interface with many +capabilities (and some limitations) that is quite popular among users. Yet, 3D +is still considered to be some kind of black magic for some users (or maybe +for the majority of users). I would thus like to explain in this post that 3D +rendering is really easy once you've understood a few concepts. To demonstrate +that, we'll render the bunny above with 60 lines of Python and one Matplotlib +call. That is, without using the 3D axis.
Advertisement: This post comes from an upcoming open access book on +scientific visualization using Python and Matplotlib. If you want to +support my work and have an early access to the book, go to +https://github.com/rougier/scientific-visualization-book.
First things first, we need to load our model. We'll use a simplified +version of the Stanford +bunny. The file uses the +wavefront format which is +one of the simplest format, so let's make a very simple (but error-prone) +loader that will just do the job for this post (and this model):
V, F = [], []
+with open("bunny.obj") as f:
+ for line in f.readlines():
+ if line.startswith('#'):
+ continue
+ values = line.split()
+ if not values:
+ continue
+ if values[0] == 'v':
+ V.append([float(x) for x in values[1:4]])
+ elif values[0] == 'f':
+ F.append([int(x) for x in values[1:4]])
+V, F = np.array(V), np.array(F)-1
+V is now a set of vertices (3D points if you prefer) and F is a set of
+faces (= triangles). Each triangle is described by 3 indices relatively to the
+vertices array. Now, let's normalize the vertices such that the overall bunny
+fits the unit box:
V = (V-(V.max(0)+V.min(0))/2)/max(V.max(0)-V.min(0))
+Now, we can have a first look at the model by getting only the x,y coordinates of the vertices and get rid of the z coordinate. To do this we can use the powerful
+PolyCollection
+object that allow to render efficiently a collection of non-regular
+polygons. Since, we want to render a bunch of triangles, this is a perfect
+match. So let's first extract the triangles and get rid of the z coordinate:
T = V[F][...,:2]
+And we can now render it:
fig = plt.figure(figsize=(6,6))
+ax = fig.add_axes([0,0,1,1], xlim=[-1,+1], ylim=[-1,+1],
+ aspect=1, frameon=False)
+collection = PolyCollection(T, closed=True, linewidth=0.1,
+ facecolor="None", edgecolor="black")
+ax.add_collection(collection)
+plt.show()
+You should obtain something like this (bunny-1.py):
The rendering we've just made is actually an orthographic +projection while the +top bunny uses a perspective projection:
In both cases, the proper way of defining a projection is first to define a +viewing volume, that is, the volume in the 3D space we want to render on the +screen. To do that, we need to consider 6 clipping planes (left, right, top, +bottom, far, near) that enclose the viewing volume (frustum) relatively to the +camera. If we define a camera position and a viewing direction, each plane can +be described by a single scalar. Once we have this viewing volume, we can +project onto the screen using either the orthographic or the perspective +projection.
Fortunately for us, these projections are quite well known and can be expressed +using 4x4 matrices:
def frustum(left, right, bottom, top, znear, zfar):
+ M = np.zeros((4, 4), dtype=np.float32)
+ M[0, 0] = +2.0 * znear / (right - left)
+ M[1, 1] = +2.0 * znear / (top - bottom)
+ M[2, 2] = -(zfar + znear) / (zfar - znear)
+ M[0, 2] = (right + left) / (right - left)
+ M[2, 1] = (top + bottom) / (top - bottom)
+ M[2, 3] = -2.0 * znear * zfar / (zfar - znear)
+ M[3, 2] = -1.0
+ return M
+
+def perspective(fovy, aspect, znear, zfar):
+ h = np.tan(0.5*radians(fovy)) * znear
+ w = h * aspect
+ return frustum(-w, w, -h, h, znear, zfar)
+For the perspective projection, we also need to specify the aperture angle that +(more or less) sets the size of the near plane relatively to the far +plane. Consequently, for high apertures, you'll get a lot of “deformations”.
However, if you look at the two functions above, you'll realize they return 4x4
+matrices while our coordinates are 3D. How to use these matrices then ? The
+answer is homogeneous
+coordinates. To make
+a long story short, homogeneous coordinates are best to deal with transformation
+and projections in 3D. In our case, because we're dealing with vertices (and
+not vectors), we only need to add 1 as the fourth coordinate (w) to all our
+vertices. Then we can apply the perspective transformation using the dot
+product.
V = np.c_[V, np.ones(len(V))] @ perspective(25,1,1,100).T
+Last step, we need to re-normalize the homogeneous coordinates. This means we
+divide each transformed vertices with the last component (w) such as to
+always have w=1 for each vertices.
V /= V[:,3].reshape(-1,1)
+Now we can display the result again (bunny-2.py):
Oh, weird result. What's wrong? What is wrong is that the camera is actually +inside the bunny. To have a proper rendering, we need to move the bunny away +from the camera or move the camera away from the bunny. Let's do the later. The +camera is currently positioned at (0,0,0) and looking up in the z direction +(because of the frustum transformation). We thus need to move the camera away a +little bit in the z negative direction and before the perspective +transformation:
V = V - (0,0,3.5)
+V = np.c_[V, np.ones(len(V))] @ perspective(25,1,1,100).T
+V /= V[:,3].reshape(-1,1)
+An now you should obtain (bunny-3.py):
It might be not obvious, but the last rendering is actually a perspective +transformation. To make it more obvious, we'll rotate the bunny around. To do +that, we need some rotation matrices (4x4) and we can as well define the +translation matrix in the meantime:
def translate(x, y, z):
+ return np.array([[1, 0, 0, x],
+ [0, 1, 0, y],
+ [0, 0, 1, z],
+ [0, 0, 0, 1]], dtype=float)
+
+def xrotate(theta):
+ t = np.pi * theta / 180
+ c, s = np.cos(t), np.sin(t)
+ return np.array([[1, 0, 0, 0],
+ [0, c, -s, 0],
+ [0, s, c, 0],
+ [0, 0, 0, 1]], dtype=float)
+
+def yrotate(theta):
+ t = np.pi * theta / 180
+ c, s = np.cos(t), np.sin(t)
+ return np.array([[ c, 0, s, 0],
+ [ 0, 1, 0, 0],
+ [-s, 0, c, 0],
+ [ 0, 0, 0, 1]], dtype=float)
+We'll now decompose the transformations we want to apply in term of model +(local transformations), view (global transformations) and projection such that +we can compute a global MVP matrix that will do everything at once:
model = xrotate(20) @ yrotate(45)
+view = translate(0,0,-3.5)
+proj = perspective(25, 1, 1, 100)
+MVP = proj @ view @ model
+and we now write:
V = np.c_[V, np.ones(len(V))] @ MVP.T
+V /= V[:,3].reshape(-1,1)
+You should obtain (bunny-4.py):
Let's now play a bit with the aperture such that you can see the difference. +Note that we also have to adapt the distance to the camera in order for the bunnies to have the same apparent size (bunny-5.py):
Let's try now to fill the triangles (bunny-6.py):
As you can see, the result is “interesting” and totally wrong. The problem is +that the PolyCollection will draw the triangles in the order they are given +while we would like to have them from back to front. This means we need to sort +them according to their depth. The good news is that we already computed this +information when we applied the MVP transformation. It is stored in the new z +coordinates. However, these z values are vertices based while we need to sort +the triangles. We'll thus take the mean z value as being representative of the +depth of a triangle. If triangles are relatively small and do not intersect, +this works beautifully:
T = V[:,:,:2]
+Z = -V[:,:,2].mean(axis=1)
+I = np.argsort(Z)
+T = T[I,:]
+And now everything is rendered right (bunny-7.py):
Let's add some colors using the depth buffer. We'll color each triangle +according to it depth. The beauty of the PolyCollection object is that you can +specify the color of each of the triangle using a NumPy array, so let's just do +that:
zmin, zmax = Z.min(), Z.max()
+Z = (Z-zmin)/(zmax-zmin)
+C = plt.get_cmap("magma")(Z)
+I = np.argsort(Z)
+T, C = T[I,:], C[I,:]
+And now everything is rendered right (bunny-8.py):
The final script is 57 lines (but hardly readable):
import numpy as np
+import matplotlib.pyplot as plt
+from matplotlib.collections import PolyCollection
+
+def frustum(left, right, bottom, top, znear, zfar):
+ M = np.zeros((4, 4), dtype=np.float32)
+ M[0, 0] = +2.0 * znear / (right - left)
+ M[1, 1] = +2.0 * znear / (top - bottom)
+ M[2, 2] = -(zfar + znear) / (zfar - znear)
+ M[0, 2] = (right + left) / (right - left)
+ M[2, 1] = (top + bottom) / (top - bottom)
+ M[2, 3] = -2.0 * znear * zfar / (zfar - znear)
+ M[3, 2] = -1.0
+ return M
+def perspective(fovy, aspect, znear, zfar):
+ h = np.tan(0.5*np.radians(fovy)) * znear
+ w = h * aspect
+ return frustum(-w, w, -h, h, znear, zfar)
+def translate(x, y, z):
+ return np.array([[1, 0, 0, x], [0, 1, 0, y],
+ [0, 0, 1, z], [0, 0, 0, 1]], dtype=float)
+def xrotate(theta):
+ t = np.pi * theta / 180
+ c, s = np.cos(t), np.sin(t)
+ return np.array([[1, 0, 0, 0], [0, c, -s, 0],
+ [0, s, c, 0], [0, 0, 0, 1]], dtype=float)
+def yrotate(theta):
+ t = np.pi * theta / 180
+ c, s = np.cos(t), np.sin(t)
+ return np.array([[ c, 0, s, 0], [ 0, 1, 0, 0],
+ [-s, 0, c, 0], [ 0, 0, 0, 1]], dtype=float)
+V, F = [], []
+with open("bunny.obj") as f:
+ for line in f.readlines():
+ if line.startswith('#'): continue
+ values = line.split()
+ if not values: continue
+ if values[0] == 'v': V.append([float(x) for x in values[1:4]])
+ elif values[0] == 'f' : F.append([int(x) for x in values[1:4]])
+V, F = np.array(V), np.array(F)-1
+V = (V-(V.max(0)+V.min(0))/2) / max(V.max(0)-V.min(0))
+MVP = perspective(25,1,1,100) @ translate(0,0,-3.5) @ xrotate(20) @ yrotate(45)
+V = np.c_[V, np.ones(len(V))] @ MVP.T
+V /= V[:,3].reshape(-1,1)
+V = V[F]
+T = V[:,:,:2]
+Z = -V[:,:,2].mean(axis=1)
+zmin, zmax = Z.min(), Z.max()
+Z = (Z-zmin)/(zmax-zmin)
+C = plt.get_cmap("magma")(Z)
+I = np.argsort(Z)
+T, C = T[I,:], C[I,:]
+fig = plt.figure(figsize=(6,6))
+ax = fig.add_axes([0,0,1,1], xlim=[-1,+1], ylim=[-1,+1], aspect=1, frameon=False)
+collection = PolyCollection(T, closed=True, linewidth=0.1, facecolor=C, edgecolor="black")
+ax.add_collection(collection)
+plt.show()
+Now it's your turn to play. Starting from this simple script, you can achieve +interesting results:
+
+
+
+
Posted +
The other day I was homeschooling my kids, and they asked me: “Daddy, can you draw us all possible non-isomorphic graphs of 3 nodes”? Or maybe I asked them that? Either way, we happily drew all possible graphs of 3 nodes, but already for 4 nodes it got hard, and for 5 nodes - plain impossible!
So I thought: let me try to write a brute-force program to do it! I spent a few hours sketching some smart dynamic programming solution to generate these graphs, and went nowhere, as apparently the problem is quite hard. I gave up, and decided to go with a naive approach:
This strategy seemed more reasonable, but writing a “graph-comparator” still felt like a cumbersome task, and more importantly, this part would itself be slow, as I'd still have to go through a whole tree of options for every graph comparison. So after some more head-scratching, I decided to simplify it even further, and use the fact that these days the memory is cheap:
For the first task, I went with the edge list, which made the task identical to generating all binary numbers of length \(\frac{N(N-1)}{2}\) with a recursive function, except instead of writing zeroes you skip edges, and instead of writing ones, you include them. Below is the function that does the trick, and has an additional bonus of listing all edges in a neat orderly way. For every edge \(i \rightarrow j\) we can be sure that \(i\) is lower than \(j\), and also that edges are sorted as words in a dictionary. Which is good, as it restricts the set of possible descriptions a bit, which will simplify our life later.
def make_graphs(n=2, i=None, j=None):
+ """Make a graph recursively, by either including, or skipping each edge.
+ Edges are given in lexicographical order by construction."""
+ out = []
+ if i is None: # First call
+ out = [[(0,1)]+r for r in make_graphs(n=n, i=0, j=1)]
+ elif j<n-1:
+ out += [[(i,j+1)]+r for r in make_graphs(n=n, i=i, j=j+1)]
+ out += [ r for r in make_graphs(n=n, i=i, j=j+1)]
+ elif i<n-1:
+ out = make_graphs(n=n, i=i+1, j=i+1)
+ else:
+ out = [[]]
+ return out
+If you run this function for a small number of nodes (say, \(N=3\)), you can see how it generates all possible graph topologies, but that some of the descriptions would actually lead to identical pictures, if drawn (graphs 2 and 3 in the list below).
[(0, 1), (0, 2), (1, 2)]
+[(0, 1), (0, 2)]
+[(0, 1), (1, 2)]
+[(0, 1)]
+Also, while building a graph from edges means that we'll never get lonely unconnected points, we can get graphs that are smaller than \(n\) nodes (the last graph in the list above), or graphs that have unconnected parts. It is impossible for \(n=3\), but starting with \(n=4\) we would get things like [(0,1), (2,3)], which is technically a graph, but you cannot exactly wear it as a piece of jewelry, as it would fall apart. So at this point I decided to only visualize fully connected graphs of exactly \(n\) vertices.
To continue with the plan, we now need to make a function that for every graph would generate a family of its “alternative representations” (given the constraints of our generator), to make sure duplicates would not slip under the radar. First we need a permutation function, to permute the nodes (you could also use a built-in function in numpy, but coding this one from scratch is always fun, isn't it?). Here's the permutation generator:
def perm(n, s=None):
+ """All permutations of n elements."""
+ if s is None: return perm(n, tuple(range(n)))
+ if not s: return [[]]
+ return [[i]+p for i in s for p in perm(n, tuple([k for k in s if k!=i]))]
+Now, for any given graph description, we can permute its nodes, sort the \(i,j\) within each edge, sort the edges themselves, remove duplicate alt-descriptions, and remember the list of potential impostors:
def permute(g, n):
+ """Create a set of all possible isomorphic codes for a graph,
+ as nice hashable tuples. All edges are i<j, and sorted lexicographically."""
+ ps = perm(n)
+ out = set([])
+ for p in ps:
+ out.add(tuple(sorted([(p[i],p[j]) if p[i]<p[j]
+ else (p[j],p[i]) for i,j in g])))
+ return list(out)
+Say, for an input description of [(0, 1), (0, 2)], the function above returns three “synonyms”:
((0, 1), (1, 2))
+((0, 1), (0, 2))
+((0, 2), (1, 2))
+I suspect there should be a neater way to code that, to avoid using the list → set → list pipeline to get rid of duplicates, but hey, it works!
At this point, the only thing that's missing is the function to check whether the graph comes in one piece, which happens to be a famous and neat algorithm called the “Union-Find". I won't describe it here in detail, but in short, it goes though all edges and connects nodes to each other in a special way; then counts how many separate connected components (like, chunks of the graph) remain in the end. If all nodes are in one chunk, we like it. If not, I don't want to see it in my pictures!
def connected(g):
+ """Check if the graph is fully connected, with Union-Find."""
+ nodes = set([i for e in g for i in e])
+ roots = {node: node for node in nodes}
+
+ def _root(node, depth=0):
+ if node==roots[node]: return (node, depth)
+ else: return _root(roots[node], depth+1)
+
+ for i,j in g:
+ ri,di = _root(i)
+ rj,dj = _root(j)
+ if ri==rj: continue
+ if di<=dj: roots[ri] = rj
+ else: roots[rj] = ri
+ return len(set([_root(node)[0] for node in nodes]))==1
+Now we can finally generate the “overkill” list of graphs, filter it, and plot the pics:
def filter(gs, target_nv):
+ """Filter all improper graphs: those with not enough nodes,
+ those not fully connected, and those isomorphic to previously considered."""
+ mem = set({})
+ gs2 = []
+ for g in gs:
+ nv = len(set([i for e in g for i in e]))
+ if nv != target_nv:
+ continue
+ if not connected(g):
+ continue
+ if tuple(g) not in mem:
+ gs2.append(g)
+ mem |= set(permute(g, target_nv))
+ return gs2
+
+# Main body
+NV = 6
+gs = make_graphs(NV)
+gs = filter(gs, NV)
+plot_graphs(gs, figsize=14, dotsize=20)
+For plotting the graphs I wrote a small wrapper for the MatPlotLib-based NetworkX visualizer, splitting the figure into lots of tiny little facets using Matplotlib subplot command. “Kamada-Kawai” layout below is a popular and fast version of a spring-based layout, that makes the graphs look really nice.
def plot_graphs(graphs, figsize=14, dotsize=20):
+ """Utility to plot a lot of graphs from an array of graphs.
+ Each graphs is a list of edges; each edge is a tuple."""
+ n = len(graphs)
+ fig = plt.figure(figsize=(figsize,figsize))
+ fig.patch.set_facecolor('white') # To make copying possible (white background)
+ k = int(np.sqrt(n))
+ for i in range(n):
+ plt.subplot(k+1,k+1,i+1)
+ g = nx.Graph() # Generate a Networkx object
+ for e in graphs[i]:
+ g.add_edge(e[0],e[1])
+ nx.draw_kamada_kawai(g, node_size=dotsize)
+ print('.', end='')
+Here are the results. To build the anticipation, let's start with something trivial: all graphs of 3 nodes:
All graphs of 4 nodes:
All graphs of 5 nodes:
Generating figures above is of course all instantaneous on a decent computer, but for 6 nodes (below) it takes a few seconds:
For 7 nodes (below) it takes about 5-10 minutes. It's easy to see why: the brute-force approach generates all \(2^{\frac{n(n-1)}{2}}\) possible graphs, which means that the number of operations grows exponentially! Every increase of \(n\) by one, gives us \(n-1\) new edges to consider, which means that the time to run the program increases by \(~2^{n-1}\). For \(n=7\) it brought me from seconds to minutes, for \(n=8\) it would have shifted me from minutes to hours, and for \(n=9\), from hours, to months of computation. Isn't it fun? We are all specialists in exponential growth these days, so here you are :)
The code is available as a Jupyter Notebook on my GitHub. I hope you enjoyed the pictures, and the read! Which of those charms above would bring most luck? Which ones seem best for divination? Let me know what you think! :)
Posted +
Cellular automata are discrete models, typically on a grid, which evolve in time. Each grid cell has a finite state, such as 0 or 1, which is updated based on a certain set of rules. A specific cell uses information of the surrounding cells, called it's neighborhood, to determine what changes should be made. In general cellular automata can be defined in any number of dimensions. A famous two dimensional example is Conway's Game of Life in which cells “live” and “die”, sometimes producing beautiful patterns.
In this post we will be looking at a one dimensional example known as elementary cellular automaton, popularized by Stephen Wolfram in the 1980s.
Imagine a row of cells, arranged side by side, each of which is colored black or white. We label black cells 1 and white cells 0, resulting in an array of bits. As an example lets consider a random array of 20 bits.
import numpy as np
+
+rng = np.random.RandomState(42)
+data = rng.randint(0, 2, 20)
+
+print(data)
+[0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 0 1 1 1 0]
+To update the state of our cellular automaton we will need to define a set of rules. +A given cell \(C\) only knows about the state of it's left and right neighbors, labeled \(L\) and \(R\) respectively. We can define a function or rule, \(f(L, C, R)\), which maps the cell state to either 0 or 1.
Since our input cells are binary values there are \(2^3=8\) possible inputs into the function.
for i in range(8):
+ print(np.binary_repr(i, 3))
+000
+001
+010
+011
+100
+101
+110
+111
+For each input triplet, we can assign 0 or 1 to the output. The output of \(f\) is the value which will replace the current cell \(C\) in the next time step. In total there are \(2^{2^3} = 2^8 = 256\) possible rules for updating a cell. Stephen Wolfram introduced a naming convention, now known as the Wolfram Code, for the update rules in which each rule is represented by an 8 bit binary number.
For example “Rule 30” could be constructed by first converting to binary and then building an array for each bit
rule_number = 30
+rule_string = np.binary_repr(rule_number, 8)
+rule = np.array([int(bit) for bit in rule_string])
+print(rule)
+[0 0 0 1 1 1 1 0]
+By convention the Wolfram code associates the leading bit with ‘111’ and the final bit with ‘000’. For rule 30 the relationship between the input, rule index and output is as follows:
for i in range(8):
+ triplet = np.binary_repr(i, 3)
+ print(f"input:{triplet}, index:{7-i}, output {rule[7-i]}")
+input:000, index:7, output 0
+input:001, index:6, output 1
+input:010, index:5, output 1
+input:011, index:4, output 1
+input:100, index:3, output 1
+input:101, index:2, output 0
+input:110, index:1, output 0
+input:111, index:0, output 0
+We can define a function which maps the input cell information with the associated rule index. Essentially we are converting the binary input to decimal and adjusting the index range.
def rule_index(triplet):
+ L, C, R = triplet
+ index = 7 - (4*L + 2*C + R)
+ return int(index)
+Now we can take in any input and look up the output based on our rule, for example:
rule[rule_index((1, 0, 1))]
+0
+Finally, we can use Numpy to create a data structure containing all the triplets for our state array and apply the function across the appropriate axis to determine our new state.
all_triplets = np.stack([
+ np.roll(data, 1),
+ data,
+ np.roll(data, -1)]
+)
+new_data = rule[np.apply_along_axis(rule_index, 0, all_triplets)]
+print(new_data)
+[1 1 1 0 1 1 1 0 1 1 1 0 0 1 1 0 1 0 0 1]
+That is the process for a single update of our cellular automata.
To do many updates and record the state over time, we will create a function.
def CA_run(initial_state, n_steps, rule_number):
+ rule_string = np.binary_repr(rule_number, 8)
+ rule = np.array([int(bit) for bit in rule_string])
+
+ m_cells = len(initial_state)
+ CA_run = np.zeros((n_steps, m_cells))
+ CA_run[0, :] = initial_state
+
+ for step in range(1, n_steps):
+ all_triplets = np.stack(
+ [
+ np.roll(CA_run[step - 1, :], 1),
+ CA_run[step - 1, :],
+ np.roll(CA_run[step - 1, :], -1),
+ ]
+ )
+ CA_run[step, :] = rule[np.apply_along_axis(rule_index, 0, all_triplets)]
+
+ return CA_run
+initial = np.array([0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0])
+data = CA_run(initial, 10, 30)
+print(data)
+[[0. 1. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 1. 0. 1. 1. 1. 0.]
+ [1. 1. 1. 0. 1. 1. 1. 0. 1. 1. 1. 0. 0. 1. 1. 0. 1. 0. 0. 1.]
+ [0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 1. 1. 1. 0. 0. 1. 1. 1. 1.]
+ [1. 0. 0. 1. 1. 1. 0. 1. 1. 1. 1. 1. 0. 0. 1. 1. 1. 0. 0. 0.]
+ [1. 1. 1. 1. 0. 0. 0. 1. 0. 0. 0. 0. 1. 1. 1. 0. 0. 1. 0. 1.]
+ [0. 0. 0. 0. 1. 0. 1. 1. 1. 0. 0. 1. 1. 0. 0. 1. 1. 1. 0. 1.]
+ [1. 0. 0. 1. 1. 0. 1. 0. 0. 1. 1. 1. 0. 1. 1. 1. 0. 0. 0. 1.]
+ [0. 1. 1. 1. 0. 0. 1. 1. 1. 1. 0. 0. 0. 1. 0. 0. 1. 0. 1. 1.]
+ [0. 1. 0. 0. 1. 1. 1. 0. 0. 0. 1. 0. 1. 1. 1. 1. 1. 0. 1. 0.]
+ [1. 1. 1. 1. 1. 0. 0. 1. 0. 1. 1. 0. 1. 0. 0. 0. 0. 0. 1. 1.]]
+For larger simulations, interesting patterns start to emerge. To visualize our simulation results we will use the ax.matshow function.
import matplotlib.pyplot as plt
+plt.rcParams['image.cmap'] = 'binary'
+
+rng = np.random.RandomState(0)
+data = CA_run(rng.randint(0, 2, 300), 150, 30)
+
+fig, ax = plt.subplots(figsize=(16, 9))
+ax.matshow(data)
+ax.axis(False);
+
With the code set up to produce the simulation, we can now start to explore the properties of these different rules. Wolfram separated the rules into four classes which are outlined below.
def plot_CA_class(rule_list, class_label):
+ rng = np.random.RandomState(seed=0)
+ fig, axs = plt.subplots(1, len(rule_list),figsize=(10, 3.5), constrained_layout=True)
+ initial = rng.randint(0, 2, 100)
+
+ for i, ax in enumerate(axs.ravel()):
+ data = CA_run(initial, 100, rule_list[i])
+ ax.set_title(f'Rule {rule_list[i]}')
+ ax.matshow(data)
+ ax.axis(False)
+
+ fig.suptitle(class_label, fontsize=16)
+
+ return fig, ax
+Cellular automata which rapidly converge to a uniform state
_ = plot_CA_class([4, 32, 172], 'Class One')
+
Cellular automata which rapidly converge to a repetitive or stable state
_ = plot_CA_class([50, 108, 173], 'Class Two')
+
Cellular automata which appear to remain in a random state
_ = plot_CA_class([60, 106, 150], 'Class Three')
+
Cellular automata which form areas of repetitive or stable states, but also form structures that interact with each other in complicated ways.
_ = plot_CA_class([54, 62, 110], 'Class Four')
+
Amazingly, the interacting structures which emerge from rule 110 has been shown to be capable of universal computation.
In all the examples above a random initial state was used, but another interesting case is when a single 1 is initialized with all other values set to zero.
initial = np.zeros(300)
+initial[300//2] = 1
+data = CA_run(initial, 150, 30)
+
+fig, ax = plt.subplots(figsize=(10, 5))
+ax.matshow(data)
+ax.axis(False);
+
For certain rules, the emergent structures interact in chaotic and interesting ways.
I hope you enjoyed this brief look into the world of elementary cellular automata, and are inspired to make some pretty pictures of your own.
Posted +
A while back, I came across this cool repository to create emoji-art from images. I wanted to use it to transform my mundane Facebook profile picture to something more snazzy. The only trouble? It was written in Rust.
So instead of going through the process of installing Rust, I decided to take the easy route and spin up some code to do the same in Python using matplotlib.
Because that's what anyone sane would do, right?
In this post, I'll try to explain my process as we attempt to recreate similar mosaics as this one below. I've aimed this post at people who've worked with some sort of image data before; but really, anyone can follow along.
import numpy as np
+from tqdm import tqdm
+from scipy import spatial
+from matplotlib import cm
+import matplotlib.pyplot as plt
+import matplotlib
+import scipy
+
+
+print(f"Matplotlib:{matplotlib.__version__}")
+print(f"Numpy:{np.__version__}")
+print(f"Scipy: {scipy.__version__}")
+
+## Matplotlib: '3.2.1'
+## Numpy: '1.18.1'
+## Scipy: '1.4.1'
+Let's read in our image:
img = plt.imread(r"naomi_32.png", 1)
+dim = img.shape[0] ##we'll need this later
+plt.imshow(img)
+
Note: The image displayed above is 100x100 but we'll use a 32x32 from here on since that's gonna suffice all our needs.
So really, what is an image? To numpy and matplotlib (and for almost every image processing library out there), it is, essentially, just a matrix (say A), where every individual pixel (p) is an element of A. If it's a grayscale image, every pixel (p) is just a single number (or a scalar) - in the range [0,1] if float, or [0,255] if integer. If it's not grayscale - like in our case - every pixel is a vector of either dimension 3 - Red (R), Green (G), and Blue (B), or dimension 4 - RGBA (A stands for Alpha, which is basically transparency).
If anything is unclear so far, I'd strongly suggest going through a post like this or this. Knowing that an image can be represented as a matrix (or a numpy array) greatly helps us as almost every transformation of the image can be represented in terms of matrix maths.
To prove my point, let's look at img a little.
+## Let's check the type of img
+print(type(img))
+# <class 'numpy.ndarray'>
+
+## The shape of the array img
+print(img.shape)
+# (32, 32, 4)
+
+## The value of the first pixel of img
+print(img[0][0])
+# [128 144 117 255]
+
+## Let's view the color of the first pixel
+fig, ax = plt.subplots()
+color=img[0][0]/255.0 ##RGBA only accepts values in the 0-1 range
+ax.fill([0, 1, 1, 0], [0, 0, 1, 1], color=color)
+That should give you a square filled with the color of the first pixel of img.
![img[0][0]](./first_pixel.png "The first pixel of the image we read in"){kind=tracking}
We want to go from a plain image to an image full of emojis - or in other words, an image of images. Essentially, we're going to replace all pixels with emojis. However, to ensure that our new emoji-image looks like the original image and not just random smiley faces, the trick is to make sure that every pixel is replaced my an emoji which has similar color to that pixel. That's what gives the result the look of a mosaic.
‘Similar’ really just means that the mean (median is also worth trying) color of the emoji should be close to the pixel it replaces.
So how do you find the mean color of an entire image? Easy. We just take all the RGBA arrays and average the Rs together, and then the Gs together, and then the Bs together, and then the As together (the As, by the way, are just all 1 in our case, so the mean is also going to be 1). Here's that idea expressed formally:
\[ (r, g, b){\mu}=\left(\frac{\left(r{1}+r_{2}+\ldots+r_{N}\right)}{N}, \frac{\left(g_{1}+g_{2}+\ldots+g_{N}\right)}{N}, \frac{\left(b_{1}+b_{2}+\ldots+b_{N}\right)}{N}\right) \]
The resulting color would be single array of RGBA values: \[ [r_{\mu}, g_{\mu}, b_{\mu}, 1] \]
So now our steps become somewhat like this:
Part I - Get emoji matches
Part II - Reshape emojis to image
That's pretty much it!
I took care of this for you beforehand with a bit of BeautifulSoup and requests magic. Our emoji collection is a numpy array of shape 1506, 16, 16, 4 - that's 1506 emojis with each being a 16x16 array of RGBA values. You can find it here.
emoji_array = np.load("emojis_16.npy")
+print(emoji_array.shape)
+## 1506, 16, 16, 4
+
+##plt.imshow(emoji_array[0]) ##to view the first emoji
+We've seen the formula above; here's the numpy code for it. We're gonna iterate over all all the 1506 emojis and create an array emoji_mean_array out of them.
emoji_mean_array = np.array([ar.mean(axis=(0,1)) for ar in emoji_array]) ##`np.median(ar, axis=(0,1))` for median instead of mean
+The easiest way to do that would be use Scipy's KDTree to create a tree object of all average RGBA values we calculated in #2. This enables us to perform fast lookup for every pixel using the query method. Here's how the code for that looks -
+tree = spatial.KDTree(emoji_mean_array)
+
+indices = []
+flattened_img = img.reshape(-1, img.shape[-1]) ##shape = [1024, 16, 16, 4]
+for pixel in tqdm(flattened_img, desc="Matching emojis"):
+ _, index=tree.query(pixel) ##returns distance and index of closest match.
+ indices.append(index)
+
+emoji_matches = emoji_array[indices] ##our emoji_matches
+The final step is to reshape the array a little more to enable us to plot it using the imshow function. As you can see above, to loop over the pixels we had to flatten the image out into the flattened_img. Now we have to sort of un-flatten it back; to make sure it's back in the form of an image. Fortunately, using numpy's reshape function makes this easy.
resized_ar = emoji_matches.reshape((dim, dim, 16, 16, 4)) ##dim is what we got earlier when we read in the image
+The last bit is the trickiest. The problem with the output we've got so far is that it's too nested. Or in simpler terms, what we have is a image where every individual pixel is itself an image. That's all fine but it's not valid input for imshow and if we try to pass it in, it tells us exactly that.
TypeError: Invalid shape (32, 32, 16, 16, 4) for image data
+To grasp our problem intuitively, think about it this way. What we have right now are lots of images like these:
What we want is to merge them all together. Like so:
To think about it slightly more technically, what we have right now is a five dimensional array. What we need is to rehshape it in such a way that it's - at maximum - three dimensional. However, it's not as easy as a simple np.reshape (I'd suggest you go ahead and try that anyway).
Don't worry though, we have Stack Overflow to the rescue! This excellent answer does exactly that. You don't have to go through it, I have copied the relevant code in here.
def np_block_2D(chops):
+ """ Converts list of chopped images to one single image"""
+ return np.block([[[x] for x in row] for row in chops])
+
+final_img = np_block_2D(resized_ar)
+
+print(final_img.shape)
+## (512, 512, 4)
+The shape looks correct enough. Let's try to plot it.
plt.imshow(final_img)
+
Et Voilà
Of course, the result looks a little meh but that's because we only used 32x32 emojis. Here's what the same code would do with 10000 emojis (100x100).
Better?
Now, let's try and create nine of these emoji-images and grid them together.
def canvas(gray_scale_img):
+ """
+ Plot a 3x3 matrix of the images using different colormaps
+ param gray_scale_img: a square gray_scale_image
+ """
+ fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(13, 8))
+ axes = axes.flatten()
+
+ cmaps = ["BuPu_r", "bone", "CMRmap", "magma", "afmhot", "ocean", "inferno", "PuRd_r", "gist_gray"]
+ for cmap, ax in zip(cmaps, axes):
+ cmapper = cm.get_cmap(cmap)
+ rgba_image = cmapper(gray_scale_img)
+ single_plot(rgba_image, ax)
+ #ax.imshow(rgba_image) ##try this if you just want to plot the plain image in different color spaces, comment the single_plot call above
+ ax.set_axis_off()
+
+ plt.subplots_adjust(hspace=0.0, wspace=-0.2)
+ return fig, axes
+The code does mostly the same stuff as before. To get the different colours, I used a simple hack. I first converted the image to grayscale and then used 9 different colormaps on it. Then I used the RGB values returned by the colormap to get the absolute values for our new input image. After that, the only part left is to just feed the new input image through the pipeline we've discussed so far and that gives us our emoji-image.
Here's what that looks like:
Pretty
Some final thoughts to wrap this up.
I'm not sure if my way to get different colours using different cmaps is what people usually do. I'm almost certain there's a better way and if you know one, please submit a PR to the repo (link below).
Iterating over every pixel is not really the best idea. We got away with it since it's just 1024 (32x32) pixels but for images with higher resolution, we'd have to either iterate over grids of images at once (say a 3x3 or 2x2 window) or resize the image itself to a more workable shape. I prefer the latter since that way we can also just resize it to a square shape in the same call which also has the additional advantage of fitting in nicely in our 3x3 mosaic. I'll leave the readers to work that out themselves using numpy (and, no, please don't use cv2.resize).
The KDTree was not part of my initial code. Initially, I'd just looped over every emoji for every pixel and then calculated the Euclidean distance (using np.linalg.norm(a-b)). As you can probably imagine, the nested loop in there slowed down the code tremendously - even a 32x32 emoji-image took around 10 minutes to run - right now the same code takes ~19 seconds. Guess that's the power of vectorization for you all.
It's worth messing around with median instead of mean to get the RGBA values of the emojis. Most emojis are circular in shape and hence there's a lot of space left outside the area of the circular region which sort of waters down the average color in turn watering down the end result. Considering the median might sort out this problem for some images which aren't very rich.
While I've tried to go in a linear manner with (what I hope was) a good mix of explanation and code, I'd strongly suggest looking at the full code in the repository here in case you feel like I sprung anything on you.
I hope you enjoyed this post and learned something from it. If you have any feedback, criticism, questions, please feel free to DM me on Twitter or email me (preferably the former since I'm almost always on there). Thank you, and take care!
Posted +
Google Summer of Code 2020 is completed. Hurray!! This post discusses about the progress so far in the three months of the coding period from 1 June to 24 August 2020 regarding the project Baseline Images Problem under matplotlib organisation under the umbrella of NumFOCUS organization.
This project helps with the difficulty in adding/modifying tests which require a baseline image. Baseline images are problematic because
So, the idea is to not store the baseline images in the repository, instead to create them from the existing tests.
We had created the matplotlib_baseline_images package. This package is involved in the sub-wheels directory so that more packages can be added in the same directory, if needed in future. The matplotlib_baseline_images package contain baseline images for both matplotlib and mpl_toolkits.
+The package can be installed by using python3 -mpip install matplotlib_baseline_images.
We successfully created the generate_missing command line flag for baseline image generation for matplotlib and mpl_toolkits in the previous months. It was generating the matplotlib and the mpl_toolkits baseline images initially. Now, we have also modified the existing flow to generate any missing baseline images, which would be fetched from the master branch on doing git pull or git checkout -b feature_branch.
Now, the image generation on the time of fresh install of matplotlib and the generation of missing baseline images works with the python3 -pytest lib/matplotlib matplotlib_baseline_image_generation for the lib/matplotlib folder and python3 -pytest lib/mpl_toolkits matplotlib_baseline_image_generation for the lib/mpl_toolkits folder.
We have written documentation explaining the following scenarios:
matplotlib_baseline_images_package to be used for testing by the developer?I am grateful to be part of such a great community. Project is really interesting and challenging :)
Thanks Thomas, Antony and Hannah for helping me to complete this project.
Posted +
Matplotlib: Revisiting Text/Font Handling
To kick things off for the final report, here's a meme to nudge about the previous blogs.
Matplotlib is a comprehensive library for creating static, animated, and interactive visualizations, which has become a de-facto Python plotting library.
Much of the implementation behind its font manager is inspired by W3C compliant algorithms, allowing users to interact with font properties like font-size, font-weight, font-family, etc.
By “not ideal”, I do not mean that the library has design flaws, but that the design was engineered in the early 2000s, and is now outdated.
(PS: here's the link to my GSoC proposal, if you're interested)
Overall, the project was divided into two major subgoals:
But before we take each of them on, we should get an idea about some basic terminology for fonts (which are a lot, and are rightly confusing)
The PR: Clarify/Improve docs on family-names vs generic-families brings about a bit of clarity about some of these terms. The next section has a linked PR which also explains the types of fonts and how that is relevant to Matplotlib.
An easy-to-read guide on Fonts and Matplotlib was created with PR: [Doc] Font Types and Font Subsetting, which is currently live at Matplotlib's DevDocs.
Taking an excerpt from one of my previous blogs (and the doc):
Fonts can be considered as a collection of these glyphs, so ultimately the goal of subsetting is to find out which glyphs are required for a certain array of characters, and embed only those within the output.
PDF, PS/EPS and SVG output document formats are special, as in the text within them can be editable, i.e, one can copy/search text from documents (for eg, from a PDF file) if the text is editable.
The PDF, PS/EPS and SVG backends used to support font subsetting, only for a few types. What that means is, before Summer ‘21, Matplotlib could generate Type 3 subsets for PDF, PS/EPS backends, but it could not generate Type 42 / TrueType subsets.
With PR: Type42 subsetting in PS/PDF merged in, users can expect their PDF/PS/EPS documents to contains subsetted glyphs from the original fonts.
This is especially benefitial for people who wish to use commercial (or CJK) fonts. Licenses for many fonts require subsetting such that they can’t be trivially copied from the output files generated from Matplotlib.
Matplotlib was designed to work with a single font at runtime. A user could specify a font.family, which was supposed to correspond to CSS properties, but that was only used to find a single font present on the user's system.
Once that font was found (which is almost always found, since Matplotlib ships with a set of default fonts), all the user text was rendered only through that font. (which used to give out “tofu” if a character wasn't found)
It might seem like an outdated approach for text rendering, now that we have these concepts like font-fallback, but these concepts weren't very well discussed in early 2000s. Even getting a single font to work was considered a hard engineering problem.
This was primarily because of the lack of any standardization for representation of fonts (Adobe had their own font representation, and so did Apple, Microsoft, etc.)
 |  |
|---|
Previous (notice Tofus) VS After (CJK font as fallback)
To migrate from a font-first approach to a text-first approach, there are multiple steps involved:
The very first (and crucial!) step is to get to a point where we have multiple font paths (ideally individual font files for the whole family). That is achieved with either:
Quoting one of my previous blogs:
Don’t break, a lot at stake!
My first approach was to change the existing public findfont API to incorporate multiple filepaths. Since Matplotlib has a very huge userbase, there's a high chance it would break a chunk of people's workflow:
+First PR (left), Second PR (right)
Once we get a list of font paths, we need to change the internal representation of a “font”. Matplotlib has a utility called FT2Font, which is written in C++, and used with wrappers as a Python extension, which in turn is used throughout the backends. For all intents and purposes, it used to mean: FT2Font === SingleFont (if you're interested, here's a meme about how FT2Font was named!)
But that is not the case anymore, here's a flowchart to explain what happens now:
+Font-Fallback Algorithm
With PR: Implement Font-Fallback in Matplotlib, every FT2Font object has a std::vector<FT2Font *> fallback_list, which is used for filling the parent cache, as can be seen in the self-explanatory flowchart.
For simplicity, only one type of cache (character -> FT2Font) is shown, whereas in actual implementation there's 2 types of caches, one shown above, and another for glyphs (glyph_id -> FT2Font).
Note: Only the parent's APIs are used in some backends, so for each of the individual public functions like
load_glyph,load_char,get_kerning, etc., we find the FT2Font object which has that glyph from the parent FT2Font cache!
Now that we have multiple fonts to render a string, we also need to embed them for those special backends (i.e., PDF/PS, etc.). This was done with some patches to specific backends:
With this, one could create a PDF or a PS/EPS document with multiple fonts which are embedded (and subsetted!).
From small contributions to eventually working on a core module of such a huge library, the road was not what I had imagined, and I learnt a lot while designing solutions to these problems.
…since all plots will work their way through the new codepath!
I think that single statement is worth the whole GSoC project.
For the sake of statistics (and to make GSoC sound a bit less intimidating), here's a list of contributions I made to Matplotlib before Summer ‘21, most of which are only a few lines of diff:
| Created At | PR Title | Diff | Status |
|---|---|---|---|
| Nov 2, 2020 | Expand ScalarMappable.set_array to accept array-like inputs | (+28 −4) | MERGED |
| Nov 8, 2020 | Add overset and underset support for mathtext | (+71 −0) | MERGED |
| Nov 14, 2020 | Strictly increasing check with test coverage for streamplot grid | (+54 −2) | MERGED |
| Jan 11, 2021 | WIP: Add support to edit subplot configurations via textbox | (+51 −11) | DRAFT |
| Jan 18, 2021 | Fix over/under mathtext symbols | (+7,459 −4,169) | MERGED |
| Feb 11, 2021 | Add overset/underset whatsnew entry | (+28 −17) | MERGED |
| May 15, 2021 | Warn user when mathtext font is used for ticks | (+28 −0) | MERGED |
Here's a list of PRs I opened during Summer'21:
From learning about software engineering fundamentals from Tom to learning about nitty-gritty details about font representations from Jouni;
From learning through Antony‘s patches and pointers to receiving amazing feedback on these blogs from Hannah, it has been an adventure! 💯
Special Mentions: Frank, Srijan and Atharva for their helping hands!
And lastly, you, the reader; if you've been following my previous blogs, or if you've landed at this one directly, I thank you nevertheless. (one last meme, I promise!)
I know I speak for every developer out there, when I say it means a lot when you choose to look at their journey or their work product; it could as well be a tiny website, or it could be as big as designing a complete library!
I'm grateful to Maptlotlib (under the parent organisation: NumFOCUS), and of course, Google Summer of Code for this incredible learning opportunity.
Farewell, reader! :')
+Consider contributing to Matplotlib (Open Source in general) ❤️
Posted +
The day of result, was a very, very long day.
With this small writeup, I intend to talk about everything before that day, my experiences, my journey, and the role of Matplotlib throughout!
I am a third-year undergraduate student currently pursuing a Dual Degree (B.Tech + M.Tech) in Information Technology at Indian Institute of Information Technology, Gwalior.
During my sophomore year, my interests started expanding in the domain of Machine Learning, where I learnt about various amazing open-source libraries like NumPy, SciPy, pandas, and Matplotlib! Gradually, in my third year, I explored the field of Computer Vision during my internship at a startup, where a big chunk of my work was to integrate their native C++ codebase to Android via JNI calls.
To actuate my learnings from the internship, I worked upon my own research along with a friend from my university. The paper was accepted in CoDS-COMAD’21 and is published at ACM Digital Library. (Link, if anyone's interested)
During this period, I also picked up the knack for open-source and started glaring at various issues (and pull requests) in libraries, including OpenCV [contributions] and NumPy [contributions].
I quickly got involved in Matplotlib’s community; it was very welcoming and beginner-friendly.
Fun fact: Its dev call was the very first I attended with people from all around the world!
We all mess up, my very first PR to an organisation like OpenCV went horrible, till date, it looks like this:
+
In all honesty, I added a single commit with only a few lines of diff.
However, I pulled all the changes from upstream
masterto my working branch, whereas the PR was to be made on3.4branch.
I'm sure I could've done tons of things to solve it, but at that time I couldn't do anything - imagine the anxiety!
At this point when I look back at those fumbled PRs, I feel like they were important for my learning process.
Fun Fact: Because of one of these initial contributions, I got a shiny little badge [Mars 2020 Helicopter Contributor] on GitHub!
It was around initial weeks of November last year, I was scanning through Good First Issue and New Feature labels, I realised a pattern - most Mathtext related issues were unattended.
To make it simple, Mathtext is a part of Matplotlib which parses mathematical expressions and provides TeX-like outputs, for example:
+
I scanned the related source code to try to figure out how to solve those Mathtext issues. Eventually, with the help of maintainers reviewing the PRs and a lot of verbose discussions on GitHub issues/pull requests and on the Gitter channel, I was able to get my initial PRs merged!
Most of us use libraries without understanding the underlining structure of them, which sometimes can cause downstream bugs!
While I was studying Matplotlib's architecture, I figured that I could use the same ideology for one of my own projects!
Matplotlib uses a global dictionary-like object named as rcParams, I used a smaller interface, similar to rcParams, in swi-ml - a small Python library I wrote, implementing a subset of ML algorithms, with a switchable backend.
It was around January, I had a conversation with one of the maintainers (hey Antony!) about the long-list of issues with the current ways of handling texts/fonts in the library.
After compiling them into an order, after few tweaks from maintainers, GSoC Idea-List for Matplotlib was born. And so did my journey of building a strong proposal!
The aim of the project is divided into 3 subgoals:
Font-Fallback: A redesigned text-first font interface - essentially parsing all family before rendering a “tofu”.
(similar to specifying font-family in CSS!)
Font Subsetting: Every exported PS/PDF would contain embedded glyphs subsetted from the whole font.
(imagine a plot with just a single letter “a”, would you like it if the PDF you exported from Matplotlib to embed the whole font file within it?)
Most mpl backends would use the unified TeX exporting mechanism
Mentors Thomas A Caswell, Antony Lee, Hannah.
Thanks a lot for spending time reading the blog! I'll be back with my progress in subsequent posts.
Posted +
“Aitik, how is your GSoC going?”
Well, it's been a while since I last wrote. But I wasn't spending time watching Loki either! (that's a lie.)
During this period the project took on some interesting (and stressful) curves, which I intend to talk about in this small writeup.
The first week of coding period, and I met one of my new mentors, Jouni. Without him, along with Tom and Antony, the project wouldn't have moved an inch.
It was initially Jouni's PR which was my starting point of the first milestone in my proposal, Font Subsetting.
As was proposed by Tom, a good way to understand something is to document your journey along the way! (well, that's what GSoC wants us to follow anyway right?)
Taking an excerpt from one of the paragraphs I wrote here:
Font Subsetting can be used before generating documents, to embed only the required glyphs within the documents. Fonts can be considered as a collection of these glyphs, so ultimately the goal of subsetting is to find out which glyphs are required for a certain array of characters, and embed only those within the output.
Now this may seem straightforward, right?
The glyph programs can call their own subprograms, for example, characters like ä could be composed by calling subprograms for a and ¨; or → could be composed by a program that changes the display matrix and calls the subprogram for ←.
Since the subsetter has to find out all such subprograms being called by every glyph included in the subset, this is a generally difficult problem!
Something which one of my mentors said which really stuck with me:
Matplotlib isn't a font library, and shouldn't try to be one.
It's really easy to fall into the trap of trying to do everything within your own project, which ends up rather hurting itself.
Since this holds true even for Matplotlib, it uses external dependencies like FreeType, ttconv, and newly proposed fontTools to handle font subsetting, embedding, rendering, and related stuff.
PS: If that font stuff didn't make sense, I would recommend going through a friendly tutorial I wrote, which is all about Matplotlib and Fonts!
Matplotlib uses an external dependency ttconv which was initially forked into Matplotlib's repository in 2003!
ttconv was a standalone commandline utility for converting TrueType fonts to subsetted Type 3 fonts (among other features) written in 1995, which Matplotlib forked in order to make it work as a library.
Over the time, there were a lot of issues with it which were either hard to fix, or didn't attract a lot of attention. (See the above paragraph for a valid reason)
One major utility which is still used is convert_ttf_to_ps, which takes a font path as input and converts it into a Type 3 or Type 42 PostScript font, which can be embedded within PS/EPS output documents. The guide I wrote (link) contains decent descriptions, the differences between these type of fonts, etc.
Why do we need to? Type 42 subsetting isn't really supported by ttconv, so we use a new dependency called fontTools, whose ‘full-time job’ is to subset Type 42 fonts for us (among other things).
It provides us with a font buffer, however ttconv expects a font path to embed that font
Easily enough, this can be done by Python's tempfile.NamedTemporaryFile:
with tempfile.NamedTemporaryFile(suffix=".ttf") as tmp:
+ # fontdata is the subsetted buffer
+ # returned from fontTools
+ tmp.write(fontdata.getvalue())
+
+ # TODO: allow convert_ttf_to_ps
+ # to input file objects (BytesIO)
+ convert_ttf_to_ps(
+ os.fsencode(tmp.name),
+ fh,
+ fonttype,
+ glyph_ids,
+ )
+But this is far from a clean API; in terms of separation of *reading* the file from *parsing* the data.
What we ideally want is to pass the buffer down to convert_ttf_to_ps, and modify the embedding code of ttconv (written in C++). And here we come across a lot of unexplored codebase, which wasn't touched a lot ever since it was forked.
Funnily enough, just yesterday, after spending a lot of quality time, me and my mentors figured out that the whole logging system of ttconv was broken, all because of a single debugging function. 🥲
This is still an ongoing problem that we need to tackle over the coming weeks, hopefully by the next time I write one of these blogs, it gets resolved!
Again, thanks a ton for spending time reading these blogs. :D
Posted +
“Well? Did you get it working?!”
Before I answer that question, if you're missing the context, check out my previous blog‘s last few lines.. promise it won't take you more than 30 seconds to get the whole problem!
With this short writeup, I intend to talk about what we did and why we did, what we did. XD
Ring any bells? Remember OS (Operating Systems)? It's one of the core CS subjects which I bunked then and regret now. (╥﹏╥)
The wikipedia page has a 2-liner explaination if you have no idea what's an Ostrich Algorithm.. but I know most of y'all won't bother clicking it XD, so here goes:
Ostrich algorithm is a strategy of ignoring potential problems by “sticking one's head in the sand and pretending there is no problem”
An important thing to note: it is used when it is more cost-effective to allow the problem to occur than to attempt its prevention.
As you might've guessed by now, we ultimately ended up with the not-so-clean API (more on this later).
The highest level overview of the problem was:
❌ fontTools -> buffer -> ttconv_with_buffer
+✅ fontTools -> buffer -> tempfile -> ttconv_with_file
+The first approach created corrupted outputs, however the second approach worked fine. A point to note here would be that Method 1 is better in terms of separation of reading the file from parsing the data.
ttconv_with_buffer is a modification to the original ttconv_with_file; that allows it to input a file buffer instead of a file-pathYou might be tempted to say:
“Well,
ttconv_with_buffermust be wrongly modified, duh.”
Logically, yes. ttconv was designed to work with a file-path and not a file-object (buffer), and modifying a codebase written in 1998 turned out to be a larger pain than we anticipated.
He even did, but the efforts to get it to production / or to fix ttconv embedding were ⋙ to just get on with the second method. That damn ostrich really helped us get out of that debugging hell. 🙃
Finally, we're onto the second subgoal for the summer: Font Fallback!
To give an idea about how things work right now:
matplotlib.rcParams["font-family"] = ["list", "of", "font", "families"]
+As soon as a font is found by iterating the font-family, all text is rendered by that and only that font.
You can immediately see the problems with this approach; using the same font for every character will not render any glyph which isn't present in that font, and will instead spit out a square rectangle called “tofu” (read the first line here).
And that is exactly the first milestone! That is, parsing the entire list of font families to get an intermediate representation of a multi-font interface.
Imagine if you had the superpower to change Python standard library's internal functions, without consulting anybody. Let's say you wanted to write a solution by hooking in and changing, let's say str("dumb") implementation by returning:
>>> str("dumb")
+["d", "u", "m", "b"]
+Pretty “dumb”, right? xD
For your usecase it might work fine, but it would also mean breaking the entire Python userbase’ workflow, not to mention the 1000000+ libraries that depend on the original functionality.
On a similar note, Matplotlib has a public API known as findfont(prop: str), which when given a string (or FontProperties) finds you a font that best matches the given properties in your system.
It is used throughout the library, as well as at multiple other places, including downstream libraries. Being naive as I was, I changed this function signature and submitted the PR. 🥲
Had an insightful discussion about this with my mentors, and soon enough raised the other PR, which didn't touch the findfont API at all.
One last thing to note: Even if we do complete the first milestone, we wouldn't be done yet, since this is just parsing the entire list to get multiple fonts..
We still need to migrate the library's internal implementation from font-first to text-first!
But that's for later, for now:
+
Posted +
“Matplotlib, I want 多个汉字 in between my text.”
Let's say you asked Matplotlib to render a plot with some label containing 多个汉字 (multiple Chinese characters) in between your English text.
Or conversely, let's say you use a Chinese font with Matplotlib, but you had English text in between (which is quite common).
Assumption: the Chinese font doesn't have those English glyphs, and vice versa
With this short writeup, I'll talk about how does a migration from a font-first to a text-first approach in Matplotlib looks like, which ideally solves the above problem.
Logically, the very first step to solving this would be to ask whether you have multiple fonts, right?
Matplotlib doesn't ship CJK (Chinese Japanese Korean) fonts, which ideally contains these Chinese glyphs. It does try to cover most grounds with the default font it ships with, however.
So if you don't have a font to render your Chinese characters, go ahead and install one! Matplotlib will find your installed fonts (after rebuilding the cache, that is).
This is where things get interesting, and what my previous writeup was all about..
Parsing the whole family to get multiple fonts for given font properties
To give you an idea about how things used to work for Matplotlib:
FT2Font is a matplotlib-to-font module, which provides high-level Python API to interact with a single font's operations like read/draw/extract/etc.
Being written in C++, the module needs wrappers around it to be converted into a Python extension using Python's C-API.
It allows us to use C++ functions directly from Python!
So wherever you see a use of font within the library (by library I mean the readable Python codebase XD), you could have derived that:
FT2Font === SingleFont
+Things are be a bit different now however..
FT2Font is basically itself a wrapper around a library called FreeType, which is a freely available software library to render fonts.
In my initial proposal.. while looking around how FT2Font is structured, I figured:
Oh, looks like all we need are Faces!
+If you don't know what faces/glyphs/ligatures are, head over to why Text Hates You. I can guarantee you'll definitely enjoy some real life examples of why text rendering is hard. 🥲
Anyway, if you already know what Faces are, it might strike you:
If we already have all the faces we need from multiple fonts (let's say we created a child of FT2Font.. which only tracks the faces for its families), we should be able to render everything from that parent FT2Font right?
As I later figured out while finding segfaults in implementing this design:
Each FT2Font is linked to a single FT_Library object!
+If you tried to load the face/glyph/character (basically anything) from a different FT2Font object.. you'll run into serious segfaults. (because one object linked to an FT_Library can't really access another object which has it's own FT_Library)
// face is linked to FT2Font; which is
+// linked to a single FT_Library object
+FT_Face face = this->get_face();
+FT_Get_Glyph(face->glyph, &placeholder); // works like a charm
+
+// somehow get another FT2Font's face
+FT_Face family_face = this->get_family_member()->get_face();
+FT_Get_Glyph(family_face->glyph, &placeholder); // segfaults!
+Realizing this took a good amount of time! After this I quickly came up with a recursive approach, wherein we:
std::vector<FT2Font *> fallback_listfallback_listA quick overhaul of the above piece of code^
bool ft_get_glyph(FT_Glyph &placeholder) {
+ FT_Error not_found = FT_Get_Glyph(this->get_face(), &placeholder);
+ if (not_found) return False;
+ else return True;
+}
+
+// within driver code
+for (uint i=0; i<fallback_list.size(); i++) {
+ // iterate through all FT2Font objects
+ bool was_found = fallback_list[i]->ft_get_glyph(placeholder);
+ if (was_found) break;
+}
+With the idea surrounding this implementation, the Agg backend is able to render a document (either through GUI, or a PNG) with multiple fonts!
I've spent days at Python C-API's argument doc, and it's hard to get what you need at first, ngl.
But, with the help of some amazing people in the GSoC community (@srijan-paul, @atharvaraykar) and amazing mentors, blockers begone!
Oh no. XD
Things work just fine for the Agg backend, but to generate a PDF/PS/SVG with multiple fonts is another story altogether! I think I'll save that for later.
Posted +
I Sidharth Bansal, was waiting for the coding period to start from the March end so that I can make my hands dirty with the code. Finally, coding period has started. Two weeks have passed. This blog contains information about the progress so far from 1 June to 14 June 2020.
Initially, we thought of creating a mpl-test and mpl package. Mpl-test package would contain the test suite and baseline images while the other package would contain parts of repository other than test and baseline-images related files and folders. +We changed our decision to creation of mpl and mpl-baseline-images packages as we don't need to create separate package for entire test suite. Our main aim was to eliminate baseline_images from the repository. Mpl-baseline-images package will contain the data[/baseline images] and related information. The other package will contain files and folders other than baseline images. +We are now trying to create the following structure for the repository:
mpl/
+ setup.py
+ lib/mpl/...
+ lib/mpl/tests/... [contains the tests .py files]
+ baseline_images/
+ setup.py
+ data/... [contains the image files]
+It will involve:
pip install mpl-baseline-images).I am creating a prototype first with two packages - main package and sub-wheel package. Once the demo app works well on Test PyPi, we can do similar changes to the main mpl repository. +The structure of demo app is analogous to the work needed for separation of baseline-images to a new package mpl-baseline-images as given below:
testrepo/
+ setup.py
+ lib/testpkg/__init__.py
+ baseline_images/setup.py
+ baseline_images/testdata.txt
+This will also include related MANIFEST files and setup.cfg.template files. The setup.py will also contain logic for exclusion of baseline-images folder from the main mpl-package.
After the current PR is merged, we will focus on eliminating the baseline-images from the mpl-baseline-images package. Then we will do similar changes for the Travis CI.
Every Tuesday and every Friday meeting is initiated at 8:30pm IST via Zoom. Meeting notes are present at HackMD.
I am grateful to be part of such a great community. Project is really interesting and challenging :) Thanks Antony and Hannah for helping me so far.
Posted +
Google Summer of Code 2020's first evaluation is about to complete. This post discusses about the progress so far in the last two weeks of the first coding period from 15 June to 30 June 2020.
We successfully created the demo app and uploaded it to the test.pypi. It contains the main and the secondary package. The main package is analogous to the matplotlib and secondary package is analogous to the matplotlib_baseline_images package as discussed in the previous blog.
I came across another way to merge the master into the branch to resolve conflicts is by rebasing the master. I understood how to create modular commits inside a pull request for easy reviewal process and better understandability of the code.
Then, we implemented the similar changes to create the matplotlib_baseline_images package. Finally, we were successful in uploading it to the test.pypi. This package is involved in the sub-wheels directory so that more packages can be added in the same directory, if needed in future. The matplotlib_baseline_images package contain baseline images for both matplotlib and mpl_toolkits.
+Some changes were required in the main matplotlib package's setup.py so that it will not take information from the packages present in the sub-wheels directory.
As baseline images are moved out of the lib/matplotlib and lib/mpl_toolkits directory. We symlinked the locations where they are used, namely in lib/matplotlib/testing/decorator.py, tools/triage_tests.py, lib/matplotlib/tests/__init__.py and lib/mpl_toolkits/tests/__init__.py.
There are some test data that is present in the baseline_images which doesn't need to be moved to the matplotlib_baseline_images package. So, that is stored under the lib/matplotlib/tests/test_data folder.
I came across the Continuous Integration tools used at mpl. We tried to install the matplotlib followed by matplotlib_baseline_images package in all three travis, appvoyer and azure-pipeline.
Once the current PR is merged, we will move to the Proposal for the baseline images problem.
Everyday meeting initiated at 11:00pm IST via Zoom. Meeting notes are present at HackMD.
I am grateful to be part of such a great community. Project is really interesting and challenging :) Thanks Antony and Hannah for helping me so far.
Posted +
Google Summer of Code 2020's first evaluation is completed. I passed!!! Hurray! Now we are in the mid way of the second evaluation. This post discusses about the progress so far in the first two weeks of the second coding period from 30 June to 12 July 2020.
We successfully created the matplotlib_baseline_images package. It contains the matplotlib and the matplotlib toolkit baseline images. Symlinking is done for the baseline images, related changes for Travis, appvoyer, azure pipelines etc. are functional and tests/test_data is created as discussed in the previous blog. PR is reviewed and suggested work is done.
We have divide the work in two parts. The first part is the generation of the baseline images discussed below. The second part is the modification of the baseline images which happens when some baseline images gets modified due to git push or git merge. Modification of baseline images will be further divided into two sub tasks: addition of new baseline image and the deletion of the previous baseline image. This will be discussed in the second half of the second phase of the Google Summer of Code 2020.
After the changes proposed in the previous PR, the developer will have no baseline images on fresh install of matplotlib. The developer would need to install the sub-wheel matplotlib_baseline_images package to get started with the testing part of the mpl. Now, we have started removing the use of the matplotlib_baseline_images package. It will require two steps as discussed above.
+The images can be generated by the image comparison tests. Once these images are generated for the first time, then they can be used as the baseline images for the later times for comparison. This is the main principle adopted. The images are first created in the result_images directory. Then they will be moved to the lib/matplotlib/tests/baseline_images directory. Later on, running the pytests will start the image comparison.
I learned about the pytest hooks and fixtures. I build a command line flag matplotlib_baseline_image_generation which will create the baseline images in the result_images directory. The full command will be python3 pytest --matplotlib_baseline_image_generation. In order to do this, we have done changes in the conftest.py and also added markers to the image_comparison decorator.
I came to know about the git worktree and the scenarios in which we can use it. I also know more about virtual environments and their need in different scenarios.
Once the generation of the baseline images is completed in the current PR, we will move to the modification of the baseline images in the second half of the second coding phase.
Monday to Thursday meeting initiated at 11:00pm IST via Zoom. Meeting notes are present at HackMD.
I am grateful to be part of such a great community. Project is really interesting and challenging :) Thanks Thomas, Antony and Hannah for helping me so far.
Posted +
Google Summer of Code 2020's second evaluation is about to complete. Now we are about to start with the final coding phase. This post discusses about the progress so far in the last two weeks of the second coding period from 13 July to 26 July 2020.
We have divided the work in two parts as discussed in the previous blog. The first part is the generation of the baseline images discussed below. The second part is the modification of the baseline images. The modification part will be implemented in the last phase of the Google Summer of Code 2020.
Now, we have started removing the use of the matplotlib_baseline_images package. After the changes proposed in the previous PR, the developer will have no baseline images on fresh install of matplotlib. So, the developer would need to generate matplotlib baseline images locally to get started with the testing part of the mpl.
+The images can be generated by the image comparison tests with use of matplotlib_baseline_image_generation flag from the command line. Once these images are generated for the first time, then they can be used as the baseline images for the later times for comparison. This is the main principle adopted.
We successfully created the matplotlib_baseline_image_generation flag in the beginning of the second evaluation but images were not created in the baseline images directory inside the matplotlib and mpl_toolkits directories, instead they were created in the result_images directory. So, we implemented this functionality. The images are created in the lib/matplotlib/tests/baseline_images directory directly now in the baseline image generation step. The baseline image generation step uses python3 -mpytest lib/matplotlib --matplotlib_baseline_image_generation command. Later on, running the pytests with python3 -mpytest lib/matplotlib will start the image comparison.
Right now, the matplotlib_baseline_image_generation flag works for the matplotlib directory. We are trying to achieve the same functionality for the mpl_toolkits directory.
Once the generation of the baseline images for mpl_toolkits directory is completed in the current PR, we will move to the modification of the baseline images in the third coding phase. The addition of new baseline image and deletion of the old baseline image will also be implemented in the last phase of GSoC. Modification of baseline images will be further divided into two sub tasks: addition of new baseline image and the deletion of the previous baseline image.
Monday to Thursday meeting initiated at 11:00pm IST via Zoom. Meeting notes are present at HackMD.
I am grateful to be part of such a great community. Project is really interesting and challenging :) Thanks Thomas, Antony and Hannah for helping me so far.
Posted +
Google Summer of Code 2020's second evaluation is completed. I passed!!! Hurray! Now we are in the mid way of the last evaluation. This post discusses about the progress so far in the first two weeks of the third coding period from 26 July to 9 August 2020.
We successfully created the matplotlib_baseline_image_generation command line flag for baseline image generation for matplotlib and mpl_toolkits in the previous months. It was generating the matplotlib and the matplotlib toolkit baseline images successfully. Now, we modified the existing flow to generate any missing baseline images, which would be fetched from the master branch on doing git pull or git checkout -b feature_branch.
We initially thought of creating a command line flag generate_baseline_images_for_test "test_a,test_b", but later on analysis of the approach, we came to the conclusion that the developer will not know about the test names to be given along with the flag. So, we tried to generate the missing images by generate_missing without the test names. This worked successfully.
Later, we refactored the matplot_baseline_image_generation and generate_missing command line flags to single command line flag matplotlib_baseline_image_generation as the logic was similar for both of them. Now, the image generation on the time of fresh install of matplotlib and the generation of missing baseline images works with the python3 -pytest lib/matplotlib matplotlib_baseline_image_generation for the lib/matplotlib folder and python3 -pytest lib/mpl_toolkits matplotlib_baseline_image_generation for the lib/mpl_toolkits folder.
We have written documentation explaining the following scenarios:
matplotlib_baseline_images_package to be used for testing by the developer?Right now, we are trying to refactor the code and maintain git clean history. The current PR is under review. I am working on the suggested changes. We are trying to merge this :)
Monday to Thursday meeting initiated at 11:00pm IST via Zoom. Meeting notes are present at HackMD.
I am grateful to be part of such a great community. Project is really interesting and challenging :) Thanks Thomas, Antony and Hannah for helping me so far.
Posted +
This year’s Google Season of Docs (GSoD) provided me the opportunity to work with the open source organization, Matplotlib. In early summer, I submitted my proposal of Developing Matplotlib Entry Paths with the goal of improving the documentation with an alternative approach to writing.
I had set out to identify with users more by providing real world contexts to examples and programming. My purpose was to lower the barrier of entry for others to begin using the Python library with an expository approach. I focused on aligning with users based on consistent derived purposes and a foundation of task-based empathy.
The project began during the community bonding phase with learning the fundamentals of building documentation and working with open source code. I later generated usability testing surveys to the community and consolidated findings. From these results, I developed two new documents for merging into the Matplotlib repository, a Getting Started introductory tutorial and a lean Style Guide for the documentation.
Throughout this year’s Season of Docs with Matplotlib, I learned a great deal about working on open source projects, provided contributions of surveying communities and interviewing subject matter experts in documentation usability testing, and produced a comprehensive introductory guide for improving entry-level content with an initiative style guide section.
As a new user to Git and GitHub, I had a learning curve in getting started with building documentation locally on my machine. Working with cloning repositories and familiarizing myself with commits and pull requests took the bulk of the first few weeks on this project. However, with experiencing errors and troubleshooting broken branches, it was excellent to be able to lean on my mentors for resolving these issues. Platforms like Gitter, Zoom, and HackMD were key in keeping communication timely and concise. I was fortunate to be able to get in touch with the team to help me as soon as I had problems.
With programming, I was not a completely fresh face to Python and Matplotlib. However, installing the library from the source and breaking down functionality to core essentials helped me grow in my understanding of not only the fundamentals, but also the terminology. Tackling everything through my own experience of using Python and then also having suggestions and advice from the development team accelerated the ideas and implementations I aimed to work towards.
New formats and standards with reStructuredText files and Sphinx compatibility were unfamiliar avenues to me at first. In building documentation and reading through already written content, I adapted to making the most of the features available with the ideas I had for writing material suited for users new to Matplotlib. Making use of tables and code examples embedded allowed me to be more flexible in visual layout and navigation.
During the beginning stages of the project, I was able to incorporate usability testing for the current documentation. By reaching out to communities on Twitter, Reddit, and various Slack channels, I compiled and consolidated findings that helped shape the language and focus of new content to create. I summarized and shared the community’s responses in addition to separate informational interviews conducted with subject matter experts in my location. These data points helped in justifying and supporting decisions for the scope and direction of the language and content.
At the end of the project, I completed our agreed upon expectations for the documentation. The focused goal consisted of a Getting Started tutorial to introduce and give context to Matplotlib for new users. In addition, through the documentation as well as the meetings with the community, we acknowledged a missing element of a Style Guide. Though a comprehensive document for the entire library was out of the scope of the project, I put together, in conjunction with the featured task, a lean version that serves as a foundational resource for writing Matplotlib documentation.
The two sections are part of a current pull request to merge into Matplotlib’s repository. I have already worked through smaller changes to the content and am working with the community in moving forward with the process.
This Season of Docs proposal began as a vision of ideals I hoped to share and work towards with an organization and has become a technical writing experience full of growth and camaraderie. I am pleased with the progress I had made and cannot thank the team enough for the leadership and mentorship they provided. It is fulfilling and rewarding to both appreciate and be appreciated within a team.
In addition, the opportunity put together by the team at Google to foster collaboration among skilled contributors cannot be understated. Highlighting the accomplishments of these new teams raises the bar for the open source community.
Special thanks to Emily Hsu, Joe McEwen, and Smriti Singh for their time and responses, fellow Matplotlib Season of Docs writer Bruno Beltran for his insight and guidance, and the Matplotlib development team mentors Tim, Tom, and Hannah for their patience, support, and approachability for helping a new technical writer like me with my own Getting Started.
My name is Jerome Villegas and I'm a technical writer based in Seattle. I've been in education and education-adjacent fields for several years before transitioning to the industry of technical communication. My career has taken me to Taiwan to teach English and work in publishing, then to New York City to work in higher education, and back to Seattle where I worked at a private school.
Since leaving my job, I've taken to supporting my family while studying technical writing at the University of Washington and supplementing the knowledge with learning programming on the side. Along with a former classmate, the two of us have worked with the UX writing community in the Pacific Northwest. We host interview sessions, moderate sessions at conferences, and generate content analyzing trends and patterns in UX/tech writing.
In telling people what I've got going on in my life, you can find work I've done at my personal site and see what we're up to at shift J. Thanks for reading!
Posted +
Matplotblog relies on your contributions to it. We want to showcase all the amazing projects that make use of Matplotlib. In this post, we will see which steps you have to follow to add a post to our blog.
To manage your contributions, we will use Git pull requests. So, if you have not done it already, you first need to fork and clone our Git repository, by clicking on the Fork button on the top right corner of the Github page, and then type the following in a terminal window:
git clone git@github.com:[USERNAME]/matplotblog.git
+where [USERNAME] should be replaced by your Github username. You now have to make sure that if you reuse this forked repository, it is up to date with the main Matplotblog repository. To do so, type the following:
git remote add upstream https://github.com/matplotlib/matplotblog.git
+You should now create a new branch, which will contain your changes. First, checkout the master:
git checkout master
+git merge upstream/master
+and then create a new branch and check it out:
cd matplotblog
+git checkout -b post-my-fancy-title
+The name of your branch should begin with post- followed by the short title of your blog post.
Then you should create a new blog post. We have used Hugo to create the Matplotblog, so you will first need to install it. To create a new post, decide a title (e.g., my-fancy-title) and type the following:
hugo new posts/my-fancy-title/index.md
+This command will create a new folder under folder_repository/posts/ called my-fancy-title. This will be your working directory for the post. If you want to add external content to your post (e.g., images), you will add it to this folder.
You can now open the file index.md in your post folder with your favorite text editor. You will see a header section delimited by —. Let us go through all the headings you can configure:
title: "Your fancy title"
+This is the title of your post that will appear at the beginning of the page. Pick a catchy one.
date: 2019-09-01T21:37:03-04:00
+The current date and time, you do not need to modify this.
draft: false
+Specify that the post is not a draft and you want it to be published right away.
description: "This is my first post contribution."
+This is a long description of the topic of your post. Modify it according to the content.
categories: ["tutorials"]
+Pick the category you want your post to be added to. You can find the list of categories in the top right menu of matplotblog (except for Home and About).
displayInList: true
+Specify that you want your post to appear in the list of latest posts and in the list of posts of the specified category.
author: Davide Valeriani
+Add your name as author. Multiple authors are also possible, separate them by commas.
resources:
+- name: featuredImage
+ src: "my-image.jpg"
+ params:
+ description: "my image description"
+ showOnTop: true
+Select an image to be associated to your post, which will appear aside the title in the homepage. Make sure to add my-image.jpg to your post folder. The parameter showOnTop decides whether or not the image will also be shown at the top of your post.
Now, you can write the main text of your post. We fully support markdown, so use it to format your post.
To preview your new post, open a terminal and type:
hugo server
+Then open the browser and visit http://localhost:1313/matplotblog to make sure your post appears in the homepage. If you spot errors or something that you want to tune, go back to your index.md file and modify it.
When your post is ready to go, you can add it to your local repository, commit and push the changes to your branch:
git add content/posts/my-fancy-title
+git commit -m "Added new blog post"
+git push
+Finally, submit a pull request to have our admins review your contribution and merge it to the master repository. To do so, type the following:
git checkout post-my-fancy-title
+git rebase master
+and then go to the page for your fork on GitHub, select your development branch, and click the pull request button. Your pull request will automatically track the changes on your development branch and update. Further info on the pull request process are available here.
That is it folks!
Posted +
This tutorial will teach you how to create custom tables in Matplotlib, which are extremely flexible in terms of the design and layout. You’ll hopefully see that the code is very straightforward! In fact, the main methods we will be using are ax.text() and ax.plot().
I want to give a lot of credit to Todd Whitehead who has created these types of tables for various Basketball teams and players. His approach to tables is nothing short of fantastic due to the simplicity in design and how he manages to effectively communicate data to his audience. I was very much inspired by his approach and wanted to be able to achieve something similar in Matplotlib.
Before I begin with the tutorial, I wanted to go through the logic behind my approach as I think it's valuable and transferable to other visualizations (and tools!).
With that, I would like you to think of tables as highly structured and organized scatterplots. Let me explain why: for me, scatterplots are the most fundamental chart type (regardless of tool).
For example ax.plot() automatically “connects the dots” to form a line chart or ax.bar() automatically “draws rectangles” across a set of coordinates. Very often (again regardless of tool) we may not always see this process happening. The point is, it is useful to think of any chart as a scatterplot or simply as a collection of shapes based on xy coordinates. This logic / thought process can unlock a ton of custom charts as the only thing you need are the coordinates (which can be mathematically computed).
With that in mind, we can move on to tables! So rather than plotting rectangles or circles we want to plot text and gridlines in a highly organized manner.
We will aim to create a table like this, which I have posted on Twitter here. Note, the only elements added outside of Matplotlib are the fancy arrows and their descriptions.
Importing required libraries.
import matplotlib as mpl
+import matplotlib.patches as patches
+from matplotlib import pyplot as plt
+First, we will need to set up a coordinate space - I like two approaches:
I want to create a coordinate space for a table containing 6 columns and 10 rows - this means (similar to pandas row/column indices) each row will have an index between 0-9 and each column will have an index between 0-6 (this is technically 1 more column than what we defined but one of the columns with a lot of text will span two column “indices”)
# first, we'll create a new figure and axis object
+fig, ax = plt.subplots(figsize=(8,6))
+
+# set the number of rows and cols for our table
+rows = 10
+cols = 6
+
+# create a coordinate system based on the number of rows/columns
+# adding a bit of padding on bottom (-1), top (1), right (0.5)
+ax.set_ylim(-1, rows + 1)
+ax.set_xlim(0, cols + .5)
+
Now, the data we want to plot is sports (football) data. We have information about 10 players and some values against a number of different metrics (which will form our columns) such as goals, shots, passes etc.
# sample data
+data = [
+ {'id': 'player10', 'shots': 1, 'passes': 79, 'goals': 0, 'assists': 1},
+ {'id': 'player9', 'shots': 2, 'passes': 72, 'goals': 0, 'assists': 1},
+ {'id': 'player8', 'shots': 3, 'passes': 47, 'goals': 0, 'assists': 0},
+ {'id': 'player7', 'shots': 4, 'passes': 99, 'goals': 0, 'assists': 5},
+ {'id': 'player6', 'shots': 5, 'passes': 84, 'goals': 1, 'assists': 4},
+ {'id': 'player5', 'shots': 6, 'passes': 56, 'goals': 2, 'assists': 0},
+ {'id': 'player4', 'shots': 7, 'passes': 67, 'goals': 0, 'assists': 3},
+ {'id': 'player3', 'shots': 8, 'passes': 91, 'goals': 1, 'assists': 1},
+ {'id': 'player2', 'shots': 9, 'passes': 75, 'goals': 3, 'assists': 2},
+ {'id': 'player1', 'shots': 10, 'passes': 70, 'goals': 4, 'assists': 0}
+]
+Next, we will start plotting the table (as a structured scatterplot). I did promise that the code will be very simple, less than 10 lines really, here it is:
# from the sample data, each dict in the list represents one row
+# each key in the dict represents a column
+for row in range(rows):
+ # extract the row data from the list
+ d = data[row]
+
+ # the y (row) coordinate is based on the row index (loop)
+ # the x (column) coordinate is defined based on the order I want to display the data in
+
+ # player name column
+ ax.text(x=.5, y=row, s=d['id'], va='center', ha='left')
+ # shots column - this is my "main" column, hence bold text
+ ax.text(x=2, y=row, s=d['shots'], va='center', ha='right', weight='bold')
+ # passes column
+ ax.text(x=3, y=row, s=d['passes'], va='center', ha='right')
+ # goals column
+ ax.text(x=4, y=row, s=d['goals'], va='center', ha='right')
+ # assists column
+ ax.text(x=5, y=row, s=d['assists'], va='center', ha='right')
+
As you can see, we are starting to get a basic wireframe of our table. Let's add column headers to further make this scatterplot look like a table.
# Add column headers
+# plot them at height y=9.75 to decrease the space to the
+# first data row (you'll see why later)
+ax.text(.5, 9.75, 'Player', weight='bold', ha='left')
+ax.text(2, 9.75, 'Shots', weight='bold', ha='right')
+ax.text(3, 9.75, 'Passes', weight='bold', ha='right')
+ax.text(4, 9.75, 'Goals', weight='bold', ha='right')
+ax.text(5, 9.75, 'Assists', weight='bold', ha='right')
+ax.text(6, 9.75, 'Special\nColumn', weight='bold', ha='right', va='bottom')
+
The rows and columns of our table are now done. The only thing that is left to do is formatting - much of this is personal choice. The following elements I think are generally useful when it comes to good table design (more research here):
Gridlines: Some level of gridlines are useful (less is more). Generally some guidance to help the audience trace their eyes or fingers across the screen can be helpful (this way we can group items too by drawing gridlines around them).
for row in range(rows):
+ ax.plot(
+ [0, cols + 1],
+ [row -.5, row - .5],
+ ls=':',
+ lw='.5',
+ c='grey'
+ )
+
+# add a main header divider
+# remember that we plotted the header row slightly closer to the first data row
+# this helps to visually separate the header row from the data rows
+# each data row is 1 unit in height, thus bringing the header closer to our
+# gridline gives it a distinctive difference.
+ax.plot([0, cols + 1], [9.5, 9.5], lw='.5', c='black')
+
Another important element for tables in my opinion is highlighting the key data points. We already bolded the values that are in the “Shots” column but we can further shade this column to give it further importance to our readers.
# highlight the column we are sorting by
+# using a rectangle patch
+rect = patches.Rectangle(
+ (1.5, -.5), # bottom left starting position (x,y)
+ .65, # width
+ 10, # height
+ ec='none',
+ fc='grey',
+ alpha=.2,
+ zorder=-1
+)
+ax.add_patch(rect)
+
We're almost there. The magic piece is ax.axis(‘off’). This hides the axis, axis ticks, labels and everything “attached” to the axes, which means our table now looks like a clean table!
ax.axis('off')
+
Adding a title is also straightforward.
ax.set_title(
+ 'A title for our table!',
+ loc='left',
+ fontsize=18,
+ weight='bold'
+)
+
Finally, if you wish to add images, sparklines, or other custom shapes and patterns then we can do this too.
To achieve this we will create new floating axes using fig.add_axes() to create a new set of floating axes based on the figure coordinates (this is different to our axes coordinate system!).
Remember that figure coordinates by default are between 0 and 1. [0,0] is the bottom left corner of the entire figure. If you’re unfamiliar with the differences between a figure and axes then check out Matplotlib's Anatomy of a Figure for further details.
newaxes = []
+for row in range(rows):
+ # offset each new axes by a set amount depending on the row
+ # this is probably the most fiddly aspect (TODO: some neater way to automate this)
+ newaxes.append(
+ fig.add_axes([.75, .725 - (row*.063), .12, .06])
+ )
+You can see below what these floating axes will look like (I say floating because they’re on top of our main axis object). The only tricky thing is figuring out the xy (figure) coordinates for these.
These floating axes behave like any other Matplotlib axes. Therefore, we have access to the same methods such as ax.bar(), ax.plot(), patches, etc. Importantly, each axis has its own independent coordinate system. We can format them as we wish.
# plot dummy data as a sparkline for illustration purposes
+# you can plot _anything_ here, images, patches, etc.
+newaxes[0].plot([0, 1, 2, 3], [1, 2, 0, 2], c='black')
+newaxes[0].set_ylim(-1, 3)
+
+# once again, the key is to hide the axis!
+newaxes[0].axis('off')
+
That’s it, custom tables in Matplotlib. I did promise very simple code and an ultra-flexible design in terms of what you want / need. You can adjust sizes, colors and pretty much anything with this approach and all you need is simply a loop that plots text in a structured and organized manner. I hope you found it useful. Link to a Google Colab notebook with the code is here
A tutorial on how to create custom tables in Matplotlib which allow for flexible design and customization.
Posted
#tutorials
UNC BIOL222: Art created with Matplotlib
Posted
#art #academia
New open access book released
Posted
#News
A tutorial on how to show usage rates and more using batteries
Posted
#tutorials
Posted +
When I, Sidharth Bansal, heard I got selected in Google Summer of Code(GSOC) 2020 with Matplotlib under Numfocus, I was jumping and dancing. In this post, I talk about my past experiences, how I got selected for GSOC with Matplotlib, and my project details. +I am grateful to the community :)
I am currently pursuing a Bachelor’s in Technology in Software Engineering at Delhi Technological University, Delhi, India. I started my journey of open source with Public Lab, an open-source organization as a full-stack Ruby on Rails web developer. I initially did the Google Summer of Code there. I built a Multi-Party Authentication System which involves authentication of the user through multiple websites linked like mapknitter.org and spectralworkbench.org with OmniAuth providers like Facebook, twitter, google, and Github. I also worked on a Multi-Tag Subscription project there. It involved tag/category subscription by the user so that users will be notified of subsequent posts in the category they subscribe to earlier. I have also mentored there as for Google Code-In and GSoC last year. I also worked there as a freelancer.
Apart from this, I also successfully completed an internship in the Google Payments team at Google, India this year as a Software Engineering Intern. I built a PAN Collection Flow there. PAN(Taxation Number) information is collected from the user if the total amount claimed by the user through Scratch cards in the current financial year exceeds PAN_LIMIT. Triggered PAN UI at the time of scratching the reward. Enabled Paisa-Offers to uplift their limit to grant Scratch Cards after crossing PAN_LIMIT. Used different technologies like Java, Guice, Android, Spanner Queues, Protocol Buffers, JUnit, etc.
I also have a keen interest in Machine Learning and Natural Language Processing and have done a couple of projects at my university. I have researched on Query Expansion using fuzzy logic. I will be publishing it in some time. It involves the fuzzification of the traditional wordnet for query expansion.
Our paper Experimental Comparison & Scientometric Inspection of Research for Word Embeddings got accepted in ESCI Journal and Springer LNN past week. It explains the ongoing trends in universal embeddings and compares them.
I chose matplotlib as it is an organization with so much cool stuff relating to plotting. I have always wanted to work on such things. People are really friendly, always eager to help!
The first step is getting involved with the community. I started using the Gitter channel to know about the maintainers. I started learning the different pieces which tie up for the baseline image problem. I started with learning the system architecture of matplotlib. Then I installed the matplotlib, learned the cool tech stack related to matplotlib like sphinx, python, pypi etc.
Learning is a continuous task. Taking guidance from mentors about the various use case scenarios involved in the GSoC project helped me to gain a lot of insights. I solved a couple of small issues. I learned about the code-review process followed here, sphinx documentation, how releases work. I did some PRs. It was a great learning experience.
The project is about the generation of baseline images instead of downloading them. The baseline images are problematic because they cause the repo size to grow rather quickly by adding more baseline images. Also, the baseline images force matplotlib contributors to pin to a somewhat old version of FreeType because nearly every release of FreeType causes tiny rasterization changes that would entail regenerating all baseline images. Thus, it causes even more repository size growth. +The idea is not to store the baseline images at all in the Github repo. It involves dividing the matplotlib package into two separate packages - mpl-test and mpl-notest. Mpl-test will have test suite and related information. The functionality of mpl plotting library will be present in mpl-notest. We will then create the logic for generating and grabbing the latest release. Some caching will be done too. We will then implement an analogous strategy to the CI.
Mentor Antony Lee
Thanks a lot for reading….having a great time coding with great people at Matplotlib. I will be right back with my work progress in subsequent posts.
Posted +
The IPCC's Special Report on Global Warming of 1.5°C (SR15), published in October 2018, +presented the latest research on anthropogenic climate change. +It was written in response to the 2015 UNFCCC's “Paris Agreement” of
holding the increase in the global average temperature to well below 2 °C +above pre-industrial levels and to pursue efforts to limit the temperature increase to 1.5 °C […]".
cf. Article 2.1.a of the Paris Agreement
As part of the SR15 assessment, an ensemble of quantitative, model-based scenarios +was compiled to underpin the scientific analysis. +Many of the headline statements widely reported by media +are based on this scenario ensemble, including the finding that
global net anthropogenic CO2 emissions decline by ~45% from 2010 levels by 2030
in all pathways limiting global warming to 1.5°C
(cf. statement C.1 in the Summary For Policymakers).
When preparing the SR15, the authors wanted to go beyond previous reports +not just regarding the scientific rigor and scope of the analysis, +but also establish new standards in terms of openness, transparency and reproducibility.
The scenario ensemble was made accessible via an interactive IAMC 1.5°C Scenario Explorer
+(link) in line with the
+FAIR principles for scientific data management and stewardship.
+The process for compiling, validating and analyzing the scenario ensemble
+was described in an open-access manuscript published in Nature Climate Change
(doi: 10.1038/s41558-018-0317-4).
In addition, the Jupyter notebooks generating many of the headline statements, +tables and figures (using Matplotlib) were released under an open-source license +to facilitate a better understanding of the analysis +and enable reuse for subsequent research. +The notebooks are available in rendered format +and on GitHub.
To facilitate reusability of the scripts and plotting utilities +developed for the SR15 analysis, we started the open-source Python package pyam +as a toolbox for working with scenarios from integrated-assessment and energy system models.
The package is a wrapper for pandas and Matplotlib +geared for several data formats commonly used in energy modelling. +Read the docs!
Posted +
Let's make up some numbers, put them in a Pandas dataframe and plot them:
import pandas as pd
+import matplotlib.pyplot as plt
+
+df = pd.DataFrame({'A': [1, 3, 9, 5, 2, 1, 1],
+ 'B': [4, 5, 5, 7, 9, 8, 6]})
+
+df.plot(marker='o')
+plt.show()
+
Not bad, but somewhat ordinary. Let's customize it by using Seaborn's dark style, as well as changing background and font colors:
plt.style.use("seaborn-dark")
+
+for param in ['figure.facecolor', 'axes.facecolor', 'savefig.facecolor']:
+ plt.rcParams[param] = '#212946' # bluish dark grey
+
+for param in ['text.color', 'axes.labelcolor', 'xtick.color', 'ytick.color']:
+ plt.rcParams[param] = '0.9' # very light grey
+
+ax.grid(color='#2A3459') # bluish dark grey, but slightly lighter than background
+
It looks more interesting now, but we need our colors to shine more against the dark background:
fig, ax = plt.subplots()
+colors = [
+ '#08F7FE', # teal/cyan
+ '#FE53BB', # pink
+ '#F5D300', # yellow
+ '#00ff41', # matrix green
+]
+df.plot(marker='o', ax=ax, color=colors)
+
Now, how to get that neon look? To make it shine, we redraw the lines multiple times, with low alpha value and slighty increasing linewidth. The overlap creates the glow effect.
n_lines = 10
+diff_linewidth = 1.05
+alpha_value = 0.03
+
+for n in range(1, n_lines+1):
+
+ df.plot(marker='o',
+ linewidth=2+(diff_linewidth*n),
+ alpha=alpha_value,
+ legend=False,
+ ax=ax,
+ color=colors)
+
For some more fine tuning, we color the area below the line (via ax.fill_between) and adjust the axis limits.
Here's the full code:
import pandas as pd
+import matplotlib.pyplot as plt
+
+
+plt.style.use("dark_background")
+
+for param in ['text.color', 'axes.labelcolor', 'xtick.color', 'ytick.color']:
+ plt.rcParams[param] = '0.9' # very light grey
+
+for param in ['figure.facecolor', 'axes.facecolor', 'savefig.facecolor']:
+ plt.rcParams[param] = '#212946' # bluish dark grey
+
+colors = [
+ '#08F7FE', # teal/cyan
+ '#FE53BB', # pink
+ '#F5D300', # yellow
+ '#00ff41', # matrix green
+]
+
+
+df = pd.DataFrame({'A': [1, 3, 9, 5, 2, 1, 1],
+ 'B': [4, 5, 5, 7, 9, 8, 6]})
+
+fig, ax = plt.subplots()
+
+df.plot(marker='o', color=colors, ax=ax)
+
+# Redraw the data with low alpha and slighty increased linewidth:
+n_shades = 10
+diff_linewidth = 1.05
+alpha_value = 0.3 / n_shades
+
+for n in range(1, n_shades+1):
+
+ df.plot(marker='o',
+ linewidth=2+(diff_linewidth*n),
+ alpha=alpha_value,
+ legend=False,
+ ax=ax,
+ color=colors)
+
+# Color the areas below the lines:
+for column, color in zip(df, colors):
+ ax.fill_between(x=df.index,
+ y1=df[column].values,
+ y2=[0] * len(df),
+ color=color,
+ alpha=0.1)
+
+ax.grid(color='#2A3459')
+
+ax.set_xlim([ax.get_xlim()[0] - 0.2, ax.get_xlim()[1] + 0.2]) # to not have the markers cut off
+ax.set_ylim(0)
+
+plt.show()
+
If this helps you or if you have constructive criticism, I'd be happy to hear about it! Please contact me via here or here. Thanks!
Posted +
Search Engine Optimization (SEO) is a process that aims to increase quantity and quality of website traffic by ensuring a website can be found in search engines for phrases that are relevant to what the site is offering. Google is the most popular search engine in the world and presence in top search results is invaluable for any online business since click rates drop exponentially with ranking position. Since the beginning, specialized entities have been decoding signals that influence position in search engine result page (SERP) focusing on e.g. number of outlinks, presence of keywords or content length. Developed practices typically resulted in better visibility, but needed to be constantly challenged because search engines introduce changes to their algorithms even every day. Since the rapid advancements in Big Data and machine learning finding significant ranking factors became increasingly more difficult. Thus, the whole SEO field required a shift where recommendations are backed up by large scale studies based on real data rather than old-fashioned practices. Whites Agency focuses strongly on Data-Driven SEO. We run many Big Data analyses which give us insights into multiple optimization opportunities.
Majority of cases we are dealing with right now focus on data harvesting and analysis. Data presentation plays an important part and since the beginning, we needed a tool that would allow us to experiment with different forms of visualizations. Because our organization is Python driven, Matplotlib was a straightforward choice for us. It is a mature project that offers flexibility and control. Among other features, Matplotlib figures can be easily exported not only to raster graphic formats (PNG, JPG) but also to vector ones (SVG, PDF, EPS), creating high-quality images that can be embedded in HTML code, LaTeX or utilized by graphic designers. In one of our projects, Matplotlib was a part of the Python processing pipeline that automatically generated PDF summaries from an HTML template for individual clients. Every data visualization project has the same core presented in the figure below, where data is loaded from the database, processed in pandas or PySpark and finally visualized with Matplotlib.
In what follows, we would like to share two insights from our studies. All figures were prepared in Matplotlib and in each case we set up a global style (overwritten if necessary):
import matplotlib.pyplot as plt
+from cycler import cycler
+
+colors = ['#00b2b8', '#fa5e00', '#404040', '#78A3B3', '#008F8F', '#ADC9D6']
+
+plt.rc('axes', grid=True, labelcolor='k', linewidth=0.8, edgecolor='#696969',
+ labelweight='medium', labelsize=18)
+plt.rc('axes.spines', left=False, right=False, top=False, bottom=True)
+plt.rc('axes.formatter', use_mathtext=True)
+
+plt.rcParams['axes.prop_cycle'] = cycler('color', colors)
+
+plt.rc('grid', alpha=1.0, color='#B2B2B2', linestyle='dotted', linewidth=1.0)
+plt.rc('xtick.major', top=False, width=0.8, size=8.0)
+plt.rc('ytick', left=False, color='k')
+plt.rcParams['xtick.color'] = 'k'
+plt.rc('font',family='Montserrat')
+plt.rcParams['font.weight'] = 'medium'
+plt.rcParams['xtick.labelsize'] = 13
+plt.rcParams['ytick.labelsize'] = 13
+plt.rcParams['lines.linewidth'] = 2.0
+Our R&D department analyzed a set of 10,000 potential customer intent phrases from the Electronics (eCommerce) and News domains (5000 phrases each). They scraped data from the Google ranking in a specific location (London, United Kingdom) both for mobile and desktop results [full study available here]. Based on those data, we distinguished TOP 20 results that appeared in SERPs. Next, each page was audited with the Google Lighthouse tool. Google Lighthouse is an open-source, automated tool for improving the quality of web pages, that among other collects information about website loading time. A single sample from our analysis which shows variations of Time to First Byte (TTFB) as a function of Google position (grouped in threes) is presented below. TTFB measures the time it takes for a user's browser to receive the first byte of page content. Regardless of the device, TTFB score is the lowest for websites that occurred in TOP 3 positions. The difference is significant, especially between TOP 3 and 4-6 results. Therefore, Google favors websites that respond fast and therefore it is advised to invest in website speed optimization.
The figure above uses fill_between function from Matplotlib library to draw colored shade that represents the 40-60th percentile range. A simple line plot with circle markers denotes the median (50th percentile). X-axis labels were assigned manually. The whole style is wrapped into a custom function that allows us to reproduce the whole figure in a single line of code. A sample is presented below:
import matplotlib.pyplot as plt
+from matplotlib.colors import LinearSegmentedColormap
+
+# --------------------------------------------
+# Set double column layout
+# --------------------------------------------
+fig, axx = plt.subplots(figsize=(20,6), ncols=2)
+
+# --------------------------------------------
+# Plot 50th percentile
+# --------------------------------------------
+line_kws = {
+ 'lw': 4.0,
+ 'marker': 'o',
+ 'ms': 9,
+ 'markerfacecolor': 'w',
+ 'markeredgewidth': 2,
+ 'c': '#00b2b8'
+}
+
+# just demonstration
+axx[0].plot(x, y, label='Electronics', **line_kws)
+
+# --------------------------------------------
+# Plot 40-60th percentile
+# --------------------------------------------
+# make color lighter
+cmap = LinearSegmentedColormap.from_list('whites', ['#FFFFFF', '#00b2b8'])
+
+# just demonstration
+axx[0].fill_between(
+ x, yl, yu,
+ color=cmap(0.5),
+ label='_nolegend_'
+)
+
+# ---------------------------------------------
+# Add x-axis labels
+# ---------------------------------------------
+# done automatically
+xtick_labels = ['1-3','4-6','7-9','10-12','13-15','16-18','19-20']
+for ax in axx:
+ ax.set_xticklabels(xtick_labels)
+
+# ----------------------------------------------
+# Export figure
+# ----------------------------------------------
+fig.savefig("lighthouse.png", bbox_inches='tight', dpi=250)
+Another example let us draw insights from Google's paid campaigns (Ads). Our R&D department scraped the first page in Google for more than 7600 queries and analyzed the ads that were present [study available only in Polish]. The queries were narrowed down to Travel category. At the moment of writing this post, each SERP can have up to 4 ads at the top and up to 3 ads at the bottom. Each ad is associated with a domain and has a headline, description, and optional extensions. Below we present TOP 25 domains with the highest visibility on desktop computers. The Y-axis shows the name of a domain and the X-axis indicates how many ads is linked with particular domain, in total. We repeated the study 3 times and aggregated the counts that is why the scale is much larger than 7600. In this project, the type of plot below allows us to summarize different brands’ ads campaign strategies and their advertising market shares. For example, itaka and wakacje have the strongest presence both on mobile and desktop and most of their ads appear at the top. The neckermann positions itself are very high, but most of their ads appear at the bottom of search results.
The figure above is a standard horizontal bar plot that can be reproduced with barh function in Matplotlib. Each y-tick has 4 different pieces (see legend). We also added automatically generated count numbers at the end of each bar for better readability. The code snippet is shown below:
import matplotlib.pyplot as plt
+import matplotlib.patches as mpatches
+from matplotlib.colors import LinearSegmentedColormap, PowerNorm
+
+# -----------------------------
+# Set default colors
+# -----------------------------
+blues = LinearSegmentedColormap.from_list(name='WhitesBlues', colors=['#FFFFFF', '#00B3B8'], gamma=1.0)
+oranges = LinearSegmentedColormap.from_list(name='WhitesOranges', colors=['#FFFFFF', '#FB5E01'], gamma=1.0)
+
+# colors
+desktop_top = blues(1.0)
+desktop_bottom = oranges(1.0)
+mobile_top = blues(0.5)
+mobile_bottom = oranges(0.5)
+
+# -----------------------------
+# Prepare Figure
+# -----------------------------
+fig, ax = plt.subplots(figsize=(10,15))
+ax.grid(False)
+
+# -----------------------------
+# Plot bars
+# -----------------------------
+# just demonstration
+
+for name in yticklabels:
+ # tmp_desktop - DataFrame with desktop data
+ # tmp_mobile - DataFrame with mobile data
+
+ ax.barh(cnt, tmp_desktop['top'], color=desktop_top, height=0.9)
+ ax.barh(cnt, tmp_desktop['bottom'], left=tmp_desktop['top'], color=desktop_bottom, height=0.9)
+ # text counter
+ ax.text(tmp_desktop['all']+100, cnt, "%d" % tmp_desktop['all'], horizontalalignment='left',
+ verticalalignment='center', fontsize=10)
+
+ ax.barh(cnt-1, tmp_mobile['top'], color=mobile_top, height=0.9)
+ ax.barh(cnt-1, tmp_mobile['bottom'], left=tmp_mobile['top'], color=mobile_bottom, height=0.9)
+ ax.text(tmp_mobile['all']+100, cnt-1, "%d" % tmp_mobile['all'], horizontalalignment='left',
+ verticalalignment='center', fontsize=10)
+
+
+ yticks.append(cnt)
+
+ cnt = cnt - 2.5
+
+# -----------------------------
+# set labels
+# -----------------------------
+ax.set_yticks(yticks)
+ax.set_yticklabels(yticklabels)
+
+# -----------------------------
+# Add legend manually
+# -----------------------------
+legend_elements = [
+ mpatches.Patch(color=desktop_top, label='desktop top'),
+ mpatches.Patch(color=desktop_bottom, label='desktop bottom'),
+ mpatches.Patch(color=mobile_top, label='mobile top'),
+ mpatches.Patch(color=mobile_bottom, label='mobile bottom')
+]
+
+ax.legend(handles=legend_elements, fontsize=15)
+This is just a sample from our studies and more can be found on our website. The Matplotlib library meets our needs in terms of visual capabilities and flexibility. It allows us to create standard plots in a single line of code, as well as experiment with different forms of graphs thanks to its lower level features. Thanks to opportunities offered by Matplotlib we may present the complicated data in a simple and reader-friendly way.
Posted +
As has been discussed in detail in Nadia Eghbal's Roads and Bridges, the CZI EOSS program +announcement, and in the NumFocus sustainability program goals, much of the critical software that science and industry are built on +is maintained by a primarily volunteer community. While this has worked, it is not sustainable in the long term for the health of many +projects or their contributors.
We are happy to announce that we have hired Elliott Sales de Andrade (QuLogic) +as the Matplotlib Software Research Engineering +Fellow supported by +the Chan Zuckerberg Initiative Essential Open Source Software for +Science +effective March 1, 2020!
Elliott has been contributing to a broad variety of Free and Open +Source projects for several years. He is an active Matplotlib +contributor and has had commit rights since October 2015. In addition +to working on Matplotlib, Elliott has contributed to a wide range of +projects in the Scientific Python software stack, both downstream and +upstream of Matplotlib, including +Cartopy, +ObsPy, and NumPy. Outside +of Python, Elliott is a developer on the Pidgin +project and a packager for Fedora +Linux. In his work on Matplotlib, he is interested in advancing +science through reproducible workflows and more accessible libraries.
We are already seeing a reduction in the backlog of open issues and +pull requests, which we hope will make the library easier to +contribute to and maintain long term. We also benefit from Elliott +having the bandwidth to maintain a library wide view of all the +on-going work and open bugs. Hiring Elliott as an RSEF is the +start of ensuring that Matplotlib is sustainable in the long term.
Looking forward to all the good work we are going to do this year!
Posted +
This is my first post for the Matplotlib blog so I wanted to lead +with an example of what I most love about it: +How much control Matplotlib gives you. +I like to use it as a programmable drawing tool that happens +to be good at plotting data.
The default layout for Matplotlib works great for a lot of things, +but sometimes you want to exert +more control. Sometimes you want to treat your figure window as +a blank canvas and create diagrams +to communicate your ideas. Here, we will walk through the process +for setting this up. Most of these tricks are detailed in +this cheat sheet for laying out plots.
import matplotlib.pyplot as plt
+import numpy as np
+The first step is to choose the size of your canvas.
(Just a heads up, I love the metaphor +of the canvas, so that's how I am using the term here. +The Canvas object is a very specific +thing in the Matplotlib code base. That's not what I'm referring to.)
I'm planning to make a diagram that is 16 centimeters wide +and 9 centimeters high. +This will fit comfortably on a piece of A4 or US Letter paper +and will be almost twice as wide as it is high. +It also scales up nicely to fit on a wide-format slide presentation.
The plt.figure() function accepts a figsize argument,
+a tuple of (width, height) in inches.
+To convert from centimeters, we'll divide by 2.54.
fig_width = 16 # cm
+fig_height = 9 # cm
+fig = plt.figure(figsize=(fig_width / 2.54, fig_height / 2.54))
+The next step is to add an Axes object that we can draw on. +By default, Matplotlib will size and place the Axes to leave +a little border and room for x- and y-axis labels. However, we don't +want that this time around. We want our Axes to extend right up +to the edge of the Figure.
The add_axes() function lets us specify exactly where to place
+our new Axes and how big to make it. It accepts a tuple of the format
+(left, bottom, width, height). The coordinate frame of the Figure
+is always (0, 0) at the bottom left corner and (1, 1) at the upper right,
+no matter what size of Figure you are working with. Positions, widths,
+and heights all become fractions of the total width and height of the Figure.
To fill the Figure with our Axes entirely, we specify a left position of 0, +a bottom position of 0, a width of 1, and a height of 1.
ax = fig.add_axes((0, 0, 1, 1))
+To make our diagram creation easier, we can set the axis limits so that +one unit in the figure equals one centimeter. This grants us +an intuitive way to control the size of objects in the diagram. +A circle with a radius of 2 will be drawn as a circle (not an ellipse) +in the final image and have a radius of 2 cm.
ax.set_xlim(0, fig_width)
+ax.set_ylim(0, fig_height)
+We can also do away with the automatically generated ticks +and tick labels with this pair of calls.
ax.tick_params(bottom=False, top=False, left=False, right=False)
+ax.tick_params(labelbottom=False, labeltop=False, labelleft=False, labelright=False)
+At this point we have a big blank space of exactly the right size and shape. +Now we can begin building our diagram. The foundation of the image will be +the background color. White is fine, but sometimes it's fun to mix it up. +Here are some ideas +to get you started.
ax.set_facecolor("antiquewhite")
+We can also add a border to the diagram to visually set it apart.
ax.spines["top"].set_color("midnightblue")
+ax.spines["bottom"].set_color("midnightblue")
+ax.spines["left"].set_color("midnightblue")
+ax.spines["right"].set_color("midnightblue")
+ax.spines["top"].set_linewidth(4)
+ax.spines["bottom"].set_linewidth(4)
+ax.spines["left"].set_linewidth(4)
+ax.spines["right"].set_linewidth(4)
+Now we have a foundation and background in place +and we're finally ready to start drawing. +You have complete freedom to +draw curves and shapes, +place points, +and add text +of any variety within our 16 x 9 garden walls.
Then when you're done, the last step is to save the figure out as a
+.png file. In this format it can be imported to and added to whatever
+document or presentation you're working on
fig.savefig("blank_diagram.png", dpi=300)
+
If you're making a collection of diagrams, +you can make a convenient template for your blank canvas.
def blank_diagram(fig_width=16, fig_height=9,
+ bg_color="antiquewhite", color="midnightblue"):
+ fig = plt.figure(figsize=(fig_width / 2.54, fig_height / 2.54))
+ ax = fig.add_axes((0, 0, 1, 1))
+ ax.set_xlim(0, fig_width)
+ ax.set_ylim(0, fig_height)
+ ax.set_facecolor(bg_color)
+
+ ax.tick_params(bottom=False, top=False,
+ left=False, right=False)
+ ax.tick_params(labelbottom=False, labeltop=False,
+ labelleft=False, labelright=False)
+
+ ax.spines["top"].set_color(color)
+ ax.spines["bottom"].set_color(color)
+ ax.spines["left"].set_color(color)
+ ax.spines["right"].set_color(color)
+ ax.spines["top"].set_linewidth(4)
+ ax.spines["bottom"].set_linewidth(4)
+ ax.spines["left"].set_linewidth(4)
+ ax.spines["right"].set_linewidth(4)
+
+ return fig, ax
+Then you can take that canvas and add arbitrary text, shapes, and lines.
fig, ax = blank_diagram()
+
+for x0 in np.arange(-3, 16, .5):
+ ax.plot([x0, x0 + 3], [0, 9], color="black")
+
+fig.savefig("stripes.png", dpi=300)
+
Or more intricately:
fig, ax = blank_diagram()
+
+centers = [(3.5, 6.5), (8, 6.5), (12.5, 6.5), (8, 2.5)]
+radii = 1.5
+texts = [
+ "\n".join(["My roommate", "is a Philistine", "and a boor"]),
+ "\n".join(["My roommate", "ate the last", "of the", "cold cereal"]),
+ "\n".join(["I am really", "really hungy"]),
+ "\n".join(["I'm annoyed", "at my roommate"]),
+]
+
+# Draw circles with text in the center
+for i, center in enumerate(centers):
+ x, y = center
+ theta = np.linspace(0, 2 * np.pi, 100)
+ ax.plot(
+ x + radii * np.cos(theta),
+ y + radii * np.sin(theta),
+ color="midnightblue",
+ )
+ ax.text(
+ x, y,
+ texts[i],
+ horizontalalignment="center",
+ verticalalignment="center",
+ color="midnightblue",
+ )
+
+# Draw arrows connecting them
+# https://e2eml.school/matplotlib_text.html#annotate
+ax.annotate(
+ "",
+ (centers[1][0] - radii, centers[1][1]),
+ (centers[0][0] + radii, centers[0][1]),
+ arrowprops=dict(arrowstyle = "-|>"),
+)
+ax.annotate(
+ "",
+ (centers[2][0] - radii, centers[2][1]),
+ (centers[1][0] + radii, centers[1][1]),
+ arrowprops=dict(arrowstyle = "-|>"),
+)
+ax.annotate(
+ "",
+ (centers[3][0] - .7 * radii, centers[3][1] + .7 * radii),
+ (centers[0][0] + .7 * radii, centers[0][1] - .7 * radii),
+ arrowprops=dict(arrowstyle = "-|>"),
+)
+ax.annotate(
+ "",
+ (centers[3][0] + .7 * radii, centers[3][1] + .7 * radii),
+ (centers[2][0] - .7 * radii, centers[2][1] - .7 * radii),
+ arrowprops=dict(arrowstyle = "-|>"),
+)
+
+fig.savefig("causal.png", dpi=300)
+
Once you get started on this path, you can start making +extravagantly annotated plots. It can elevate your data +presentations to true storytelling.
Happy diagram building!
Advocating is all about communicating facts clearly. I used Matplotlib to show the financial struggles of postdocs in the Boston area.
Posted
#academia
See how you can contribute to the matplotblog.
Posted
#tutorials
Matplotblog, the new blog of Matplotlib, to showcase and share great visualization stories.
Posted
#editorial
Google Summer of Code 2021: Final Report - Aitik Gupta
Posted
#News #GSoC
Quarter Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
The Python Graph Gallery is a website that displays hundreds of chart examples made with python. It goes from very basic to highly customized examples and is based on common viz libraries like matplotlib, seaborn or plotly.
Posted
#tutorials #graphs
Pre-Quarter Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
Mid-Term Progress with Google Summer of Code 2021 project under NumFOCUS: Aitik Gupta
Posted
#News #GSoC
Introduction about Aitik Gupta, Google Summer of Code 2021 Intern under the parent organisation: NumFOCUS
Posted
#News #GSoC
Learn how to create a simple stellar chart, an alternative to the radar chart.
Posted
#tutorials
Many figures in the IPCC SR15 were generated using Matplotlib. +The data and open-source notebooks were published to increase the transparency and reproducibility of the analysis.
Posted
#academia #tutorials
This is my first post contribution to Matplotlib.
Posted
#GSoD
Learn how to easily create step charts through examining the multilingualism of pop group WayV
Posted
#tutorials #graphs
Final Work Product Report for the Google Summer of Code 2020 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the first half of the Google Summer of Code 2020 Phase 3 for the Baseline Images Problem
Posted
#News #GSoC
Progress Report for the second half of the Google Summer of Code 2020 Phase 2 for the Baseline Images Problem
Posted
#News #GSoC
A brief tour through the world of elementary cellular automata
Posted
#tutorials
Progress Report for the first half of the Google Summer of Code 2020 Phase 2 for the Baseline Images Problem
Posted
#News #GSoC
Discover the bizarre geometry of the fractals and learn how to make an animated visualization of these marvels using Python and the Matplotlib's Animation API.
Posted
#tutorials
Progress Report for the second half of the Google Summer of Code 2020 Phase 1 for the Baseline Images Problem
Posted
#News #GSoC
This post describes how to animate some oceanographic measurements in a tweaked polar plot
Posted
#tutorials
Progress Report for the first half of the Google Summer of Code 2020 Phase 1 for the Baseline Images Problem
Posted
#News #GSoC
This post describes the difference between the pyplot and object oriented interface to make plots.
Posted
Applied image manipulation to create procedural art.
Posted
#tutorials #art
A fun project about drawing all possible differently-looking (not isomorphic) graphs of N nodes.
Posted
#tutorials #graphs
Introductory post about Sidharth Bansal, Google Summer of Code 2020 Intern for Baseline Image Problem Project under Numfocus
Posted
#News #GSoC
Futuristic neon glow for your next data visualization
Posted
#tutorials
We have hired Elliott Sales de Andrade as the Matplotlib Software Research Engineering Fellow supported by the Chan Zuckerberg Initiative Essential Open Source Software for Science
Posted
#News
How to use Matplotlib to make diagrams.
Posted
#tutorials
This post details how to leverage gridspec to create ridgeplots in Matplotlib
Posted
#tutorials
Learn how to create a Tesla Cybertruck with Matplotlib that drives via animation.
Posted
#tutorials
This guide dives deep into the inner workings of Matplotlib's Figures, Axes, subplots and the very amazing GridSpec!
Posted
#tutorials
3D rendering is really easy once you've understood a few concepts. To demonstrate that, we'll design a simple custom 3D engine that with 60 lines of Python and one Matplotlib call. That is, we'll render the bunny without using the 3D axis.
Posted
#tutorials #3D
At Whites Agency we analyze big unstructured data to increases client's online visibility. We share our story of how we used Matplotlib to present the complicated data in a simple and reader-friendly way.
Posted
#industry
Ed Hawkins made this impressively simple plot to show how global temperatures have risen since 1880. Here is how to recreate it using Matplotlib.
Posted
#tutorials #academia
Posted +
To get acquainted with the basics of plotting with matplotlib, let's try plotting how much distance an object under free-fall travels with respect to time and also, its velocity at each time step.
If, you have ever studied physics, you can tell that is a classic case of Newton's equations of motion, where
$$ v = a \times t $$
$$ S = 0.5 \times a \times t^{2} $$
We will assume an initial velocity of zero.
import numpy as np
+
+time = np.arange(0., 10., 0.2)
+velocity = np.zeros_like(time, dtype=float)
+distance = np.zeros_like(time, dtype=float)
+We know that under free-fall, all objects move with the constant acceleration of $$g = 9.8~m/s^2$$
g = 9.8 # m/s^2
+
+velocity = g * time
+distance = 0.5 * g * np.power(time, 2)
+The above code gives us two numpy arrays populated with the distance and velocity data points.
When using matplotlib we have two approaches:
pyplot interface / functional interface.matplotlib on the surface is made to imitate MATLAB's method of generating plots, which is called pyplot. All the pyplot commands make changes and modify the same figure. This is a state-based interface, where the state (i.e., the figure) is preserved through various function calls (i.e., the methods that modify the figure). This interface allows us to quickly and easily generate plots. The state-based nature of the interface allows us to add elements and/or modify the plot as we need, when we need it.
This interface shares a lot of similarities in syntax and methodology with MATLAB. For example, if we want to plot a blue line where each data point is marked with a circle, we can use the string 'bo-'.
import matplotlib.pyplot as plt
+
+plt.figure(figsize=(9,7), dpi=100)
+plt.plot(time,distance,'bo-')
+plt.xlabel("Time")
+plt.ylabel("Distance")
+plt.legend(["Distance"])
+plt.grid(True)
+The plot shows how much distance was covered by the free-falling object with each passing second.
plt.figure(figsize=(9,7), dpi=100)
+plt.plot(time, velocity,'go-')
+plt.xlabel("Time")
+plt.ylabel("Velocity")
+plt.legend(["Velocity"])
+plt.grid(True)
+The plot below shows us how the velocity is increasing.
Let's try to see what kind of plot we get when we plot both distance and velocity in the same plot.
plt.figure(figsize=(9,7), dpi=100)
+plt.plot(time, velocity,'g-')
+plt.plot(time, distance,'b-')
+plt.ylabel("Distance and Velocity")
+plt.xlabel("Time")
+plt.legend(["Distance", "Velocity"])
+plt.grid(True)
+
Here, we run into some obvious and serious issues. We can see that since both the quantities share the same axis but have very different magnitudes, the graph looks disproportionate. What we need to do is separate the two quantities on two different axes. This is where the second approach to making plot comes into play.
Also, the pyplot approach doesn't really scale when we are required to make multiple plots or when we have to make intricate plots that require a lot of customisation. However, internally matplotlib has an Object-Oriented interface that can be accessed just as easily, which allows to reuse objects.
When using the OO interface, it helps to know how the matplotlib structures its plots. The final plot that we see as the output is a ‘Figure’ object. The Figure object is the top level container for all the other elements that make up the graphic image. These “other” elements are called Artists. The Figure object can be thought of as a canvas, upon which different artists act to create the final graphic image. This Figure can contain any number of various artists.
Things to note about the anatomy of a figure are:
Artists. Artists are basically all the elements that are rendered onto the figure. This can include text, patches (like arrows and shapes), etc. Thus, all the following Figure, Axes and Axis objects are also Artists.Axes object. The Axes object holds the actual data that we are going to display. It will also contain X- and Y-axis labels, a title. Each Axes object will contain two or more Axis objects.Axis objects set the data limits. It also contains the ticks and ticks labels. ticks are the marks that we see on a axis.Understanding this hierarchy of Figure, Artist, Axes and Axis is immensely important, because it plays a crucial role in how me make an animation in matplotlib.
Now that we understand how plots are generated, we can easily solve the problem we faced earlier. To make Velocity and Distance plot to make more sense, we need to plot each data item against a seperate axis, with a different scale. Thus, we will need one parent Figure object and two Axes objects.
fig, ax1 = plt.subplots()
+
+ax1.set_ylabel("distance (m)")
+ax1.set_xlabel("time")
+ax1.plot(time, distance, "blue")
+
+ax2 = ax1.twinx() # create another y-axis sharing a common x-axis
+
+ax2.set_ylabel("velocity (m/s)")
+ax2.set_xlabel("time")
+ax2.plot(time, velocity, "green")
+
+fig.set_size_inches(7,5)
+fig.set_dpi(100)
+
+plt.show()
+
This plot is still not very intuitive. We should add a grid and a legend. Perhaps, we can also change the color of the axis labels and tick labels to the color of the lines.
But, something very weird happens when we try to turn on the grid, which you can see here at Cell 8. The grid lines don't align with the tick labels on the both the Y-axes. We can see that tick values matplotlib is calculating on its own are not suitable to our needs and, thus, we will have to calculate them ourselves.
fig, ax1 = plt.subplots()
+
+ax1.set_ylabel("distance (m)", color="blue")
+ax1.set_xlabel("time")
+ax1.plot(time, distance, "blue")
+ax1.set_yticks(np.linspace(*ax1.get_ybound(), 10))
+ax1.tick_params(axis="y", labelcolor="blue")
+ax1.xaxis.grid()
+ax1.yaxis.grid()
+
+ax2 = ax1.twinx() # create another y-axis sharing a common x-axis
+
+ax2.set_ylabel("velocity (m/s)", color="green")
+ax2.set_xlabel("time")
+
+ax2.tick_params(axis="y", labelcolor="green")
+ax2.plot(time, velocity, "green")
+ax2.set_yticks(np.linspace(*ax2.get_ybound(), 10))
+
+fig.set_size_inches(7,5)
+fig.set_dpi(100)
+fig.legend(["Distance", "Velocity"])
+plt.show()
+The command ax1.set_yticks(np.linspace(*ax1.get_ybound(), 10)) calculates the tick values for us. Let's break this down to see what is happening:
np.linspace command will create a set of n no. of partitions between a specified upper and lower limit.ax1.get_ybound() returns a list which contains the maximum and minimum limits for that particular axis (which in our case is the Y-axis).* acts as an unpacking operator when prepended before a list or tuple. Thus, it will convert a list [1, 2, 3, 4] into seperate values 1, 2, 3, 4. This is an immensely powerful feature.np.linspace method to divide the interval between the maximum and minimum tick values into 10 equal parts.set_yticks method.The same process is repeated for the second axis.
In this part, we covered some basics of matplotlib plotting, covering the basic two approaches of how to make plots. In the next part, we will cover how to make simple animations. If you like the content of this blog post, or you have any suggestions or comments, drop me an email or tweet or ping me on IRC. Nowadays, you will find me hanging around #matplotlib on Freenode. Thanks!
This post is part of a series I'm doing on my personal blog. This series is basically going to be about how to animate stuff using python's matplotlib library. matplotlib has an excellent documentation where you can find a detailed documentation on each of the methods I have used in this blog post. Also, I will be publishing each part of this series in the form of a jupyter notebook, which can be found here.
The series will have three posts which will cover:
matplotlib.FuncAnimation.I would like to say a few words about the methodology of these series:
Posted +
Data visualization is a key step in a data science pipeline. Python offers great possibilities when it comes to representing some data graphically, but it can be hard and time-consuming to create the appropriate chart.
The Python Graph Gallery is here to help. It displays many examples, always providing the reproducible code. It allows to build the desired chart in minutes.
The gallery currently provides more than 400 chart examples. Those examples are organized in 40 sections, one for each chart types: scatterplot, boxplot, barplot, treemap and so on. Those chart types are organized in 7 big families as suggested by data-to-viz.com: one for each visualization purpose.
It is important to note that not only the most common chart types are covered. Lesser known charts like chord diagrams, streamgraphs or bubble maps are also available.
Each section always starts with some very basic examples. It allows to understand how to build a chart type in a few seconds. Hopefully applying the same technique on another dataset will thus be very quick.
For instance, the scatterplot section starts with this matplotlib example. It shows how to create a dataset with pandas and plot it with the plot() function. The main graph argument like linestyle and marker are described to make sure the code is understandable.
The gallery uses several libraries like seaborn or plotly to produce its charts, but is mainly focus on matplotlib. Matplotlib comes with great flexibility and allows to build any kind of chart without limits.
A whole page is dedicated to matplotlib. It describes how to solve recurring issues like customizing axes or titles, adding annotations (see below) or even using custom fonts.
The gallery is also full of non-straightforward examples. For instance, it has a tutorial explaining how to build a streamchart with matplotlib. It is based on the stackplot() function and adds some smoothing to it:
Last but not least, the gallery also displays some publication ready charts. They usually involve a lot of matplotlib code, but showcase the fine grain control one has over a plot.
Here is an example with a post inspired by Tuo Wang‘s work for the tidyTuesday project. (Code translated from R available here)
The python graph gallery is an ever growing project. It is open-source, with all its related code hosted on github.
Contributions are very welcome to the gallery. Each blogpost is just a jupyter notebook so suggestion should be very easy to do through issues or pull requests!
The python graph gallery is a project developed by Yan Holtz in his free time. It can help you improve your technical skills when it comes to visualizing data with python.
The gallery belongs to an ecosystem of educative websites. Data to viz describes best practices in data visualization, the R, python and d3.js graph galleries provide technical help to build charts with the 3 most common tools.
For any question regarding the project, please say hi on twitter at @R_Graph_Gallery!
Posted +
In May 2020, Alexandre Morin-Chassé published a blog post about the stellar chart. This type of chart is an (approximately) direct alternative to the radar chart (also known as web, spider, star, or cobweb chart) — you can read more about this chart here.
In this tutorial, we will see how we can create a quick-and-dirty stellar chart. First of all, let's get the necessary modules/libraries, as well as prepare a dummy dataset (with just a single record).
from itertools import chain, zip_longest
+from math import ceil, pi
+
+import matplotlib.pyplot as plt
+
+data = [
+ ("V1", 8),
+ ("V2", 10),
+ ("V3", 9),
+ ("V4", 12),
+ ("V5", 6),
+ ("V6", 14),
+ ("V7", 15),
+ ("V8", 25),
+]
+We will also need some helper functions, namely a function to round up to the nearest 10 (round_up()) and a function to join two sequences (even_odd_merge()). In the latter, the values of the first sequence (a list or a tuple, basically) will fill the even positions and the values of the second the odd ones.
def round_up(value):
+ """
+ >>> round_up(25)
+ 30
+ """
+ return int(ceil(value / 10.0)) * 10
+
+
+def even_odd_merge(even, odd, filter_none=True):
+ """
+ >>> list(even_odd_merge([1,3], [2,4]))
+ [1, 2, 3, 4]
+ """
+ if filter_none:
+ return filter(None.__ne__, chain.from_iterable(zip_longest(even, odd)))
+
+ return chain.from_iterable(zip_longest(even, odd))
+That said, to plot data on a stellar chart, we need to apply some transformations, as well as calculate some auxiliary values. So, let's start by creating a function (prepare_angles()) to calculate the angle of each axis on the chart (N corresponds to the number of variables to be plotted).
def prepare_angles(N):
+ angles = [n / N * 2 * pi for n in range(N)]
+
+ # Repeat the first angle to close the circle
+ angles += angles[:1]
+
+ return angles
+Next, we need a function (prepare_data()) responsible for adjusting the original data (data) and separating it into several easy-to-use objects.
def prepare_data(data):
+ labels = [d[0] for d in data] # Variable names
+ values = [d[1] for d in data]
+
+ # Repeat the first value to close the circle
+ values += values[:1]
+
+ N = len(labels)
+ angles = prepare_angles(N)
+
+ return labels, values, angles, N
+Lastly, for this specific type of chart, we require a function (prepare_stellar_aux_data()) that, from the previously calculated angles, prepares two lists of auxiliary values: a list of intermediate angles for each pair of angles (stellar_angles) and a list of small constant values (stellar_values), which will act as the values of the variables to be plotted in order to achieve the star-like shape intended for the stellar chart.
def prepare_stellar_aux_data(angles, ymax, N):
+ angle_midpoint = pi / N
+
+ stellar_angles = [angle + angle_midpoint for angle in angles[:-1]]
+ stellar_values = [0.05 * ymax] * N
+
+ return stellar_angles, stellar_values
+At this point, we already have all the necessary ingredients for the stellar chart, so let's move on to the Matplotlib side of this tutorial. In terms of aesthetics, we can rely on a function (draw_peripherals()) designed for this specific purpose (feel free to customize it!).
def draw_peripherals(ax, labels, angles, ymax, outer_color, inner_color):
+ # X-axis
+ ax.set_xticks(angles[:-1])
+ ax.set_xticklabels(labels, color=outer_color, size=8)
+
+ # Y-axis
+ ax.set_yticks(range(10, ymax, 10))
+ ax.set_yticklabels(range(10, ymax, 10), color=inner_color, size=7)
+ ax.set_ylim(0, ymax)
+ ax.set_rlabel_position(0)
+
+ # Both axes
+ ax.set_axisbelow(True)
+
+ # Boundary line
+ ax.spines["polar"].set_color(outer_color)
+
+ # Grid lines
+ ax.xaxis.grid(True, color=inner_color, linestyle="-")
+ ax.yaxis.grid(True, color=inner_color, linestyle="-")
+To plot the data and orchestrate (almost) all the steps necessary to have a stellar chart, we just need one last function: draw_stellar().
def draw_stellar(
+ ax,
+ labels,
+ values,
+ angles,
+ N,
+ shape_color="tab:blue",
+ outer_color="slategrey",
+ inner_color="lightgrey",
+):
+ # Limit the Y-axis according to the data to be plotted
+ ymax = round_up(max(values))
+
+ # Get the lists of angles and variable values
+ # with the necessary auxiliary values injected
+ stellar_angles, stellar_values = prepare_stellar_aux_data(angles, ymax, N)
+ all_angles = list(even_odd_merge(angles, stellar_angles))
+ all_values = list(even_odd_merge(values, stellar_values))
+
+ # Apply the desired style to the figure elements
+ draw_peripherals(ax, labels, angles, ymax, outer_color, inner_color)
+
+ # Draw (and fill) the star-shaped outer line/area
+ ax.plot(
+ all_angles,
+ all_values,
+ linewidth=1,
+ linestyle="solid",
+ solid_joinstyle="round",
+ color=shape_color,
+ )
+
+ ax.fill(all_angles, all_values, shape_color)
+
+ # Add a small hole in the center of the chart
+ ax.plot(0, 0, marker="o", color="white", markersize=3)
+Finally, let's get our chart on a blank canvas (figure).
fig = plt.figure(dpi=100)
+ax = fig.add_subplot(111, polar=True) # Don't forget the projection!
+
+draw_stellar(ax, *prepare_data(data))
+
+plt.show()
+
It's done! Right now, you have an example of a stellar chart and the boilerplate code to add this type of chart to your repertoire. If you end up creating your own stellar charts, feel free to share them with the world (and me!). I hope this tutorial was useful and interesting for you!
Posted +
As part of the University of North Carolina BIOL222 class, Dr. Catherine Kehl asked her students to “use matplotlib.pyplot to make art.” BIOL222 is Introduction to Programming, aimed at students with no programming background. The emphasis is on practical, hands-on active learning.
The students completed the assignment with festive enthusiasm around Halloween. Here are some great examples:
Harris Davis showed an affinity for pumpkins, opting to go 3D!
+
# get library for 3d plotting
+from mpl_toolkits.mplot3d import Axes3D
+
+# make a pumpkin :)
+rho = np.linspace(0, 3*np.pi,32)
+theta, phi = np.meshgrid(rho, rho)
+r, R = .5, .5
+X = (R + r * np.cos(phi)) * np.cos(theta)
+Y = (R + r * np.cos(phi)) * np.sin(theta)
+Z = r * np.sin(phi)
+
+# make the stem
+theta1 = np.linspace(0,2*np.pi,90)
+r1 = np.linspace(0,3,50)
+T1, R1 = np.meshgrid(theta1, r1)
+X1 = R1 * .5*np.sin(T1)
+Y1 = R1 * .5*np.cos(T1)
+Z1 = -(np.sqrt(X1**2 + Y1**2) - .7)
+Z1[Z1 < .3] = np.nan
+Z1[Z1 > .7] = np.nan
+
+# Display the pumpkin & stem
+fig = plt.figure()
+ax = fig.gca(projection = '3d')
+ax.set_xlim3d(-1, 1)
+ax.set_ylim3d(-1, 1)
+ax.set_zlim3d(-1, 1)
+ax.plot_surface(X, Y, Z, color = 'tab:orange', rstride = 1, cstride = 1)
+ax.plot_surface(X1, Y1, Z1, color = 'tab:green', rstride = 1, cstride = 1)
+plt.show()
+Bryce Desantis stuck to the biological theme and demonstrated fractal art.
+
import numpy as np
+import matplotlib.pyplot as plt
+
+#Barnsley's Fern - Fractal; en.wikipedia.org/wiki/Barnsley_…
+
+#functions for each part of fern:
+#stem
+def stem(x,y):
+ return (0, 0.16*y)
+#smaller leaflets
+def smallLeaf(x,y):
+ return (0.85*x + 0.04*y, -0.04*x + 0.85*y + 1.6)
+#large left leaflets
+def leftLarge(x,y):
+ return (0.2*x - 0.26*y, 0.23*x + 0.22*y + 1.6)
+#large right leftlets
+def rightLarge(x,y):
+ return (-0.15*x + 0.28*y, 0.26*x + 0.24*y + 0.44)
+componentFunctions = [stem, smallLeaf, leftLarge, rightLarge]
+
+# number of data points and frequencies for parts of fern generated:
+#lists with all 75000 datapoints
+datapoints = 75000
+x, y = 0, 0
+datapointsX = []
+datapointsY = []
+#For 75,000 datapoints
+for n in range(datapoints):
+ FrequencyFunction = np.random.choice(componentFunctions, p=[0.01, 0.85, 0.07, 0.07])
+ x, y = FrequencyFunction(x,y)
+ datapointsX.append(x)
+ datapointsY.append(y)
+
+#Scatter plot & scaled down to 0.1 to show more definition:
+plt.scatter(datapointsX,datapointsY,s=0.1, color='g')
+#Title of Figure
+plt.title("Barnsley's Fern - Assignment 3")
+#Changing background color
+ax = plt.axes()
+ax.set_facecolor("#d8d7bf")
+Grace Bell got a little trippy with this rotationally semetric art. It's pretty cool how she captured mouse events. It reminds us of a flower. What do you see?
+
import matplotlib.pyplot as plt
+from matplotlib.tri import Triangulation
+from matplotlib.patches import Polygon
+import numpy as np
+
+#I found this sample code online and manipulated it to make the art piece!
+#was interested in because it combined what we used for functions as well as what we used for plotting with (x,y)
+def update_polygon(tri):
+ if tri == -1:
+ points = [0, 0, 0]
+ else:
+ points = triang.triangles[tri]
+ xs = triang.x[points]
+ ys = triang.y[points]
+ polygon.set_xy(np.column_stack([xs, ys]))
+
+def on_mouse_move(event):
+ if event.inaxes is None:
+ tri = -1
+ else:
+ tri = trifinder(event.xdata, event.ydata)
+ update_polygon(tri)
+ ax.set_title(f'In triangle {tri}')
+ event.canvas.draw()
+#this is the info that creates the angles
+n_angles = 14
+n_radii = 7
+min_radius = 0.1 #the radius of the middle circle can move with this variable
+radii = np.linspace(min_radius, 0.95, n_radii)
+angles = np.linspace(0, 2 * np.pi, n_angles, endpoint=False)
+angles = np.repeat(angles[..., np.newaxis], n_radii, axis=1)
+angles[:, 1::2] += np.pi / n_angles
+x = (radii*np.cos(angles)).flatten()
+y = (radii*np.sin(angles)).flatten()
+triang = Triangulation(x, y)
+triang.set_mask(np.hypot(x[triang.triangles].mean(axis=1),
+ y[triang.triangles].mean(axis=1))
+ < min_radius)
+
+trifinder = triang.get_trifinder()
+
+fig, ax = plt.subplots(subplot_kw={'aspect': 'equal'})
+ax.triplot(triang, 'y+-') #made the color of the plot yellow and there are "+" for the data points but you can't really see them because of the lines crossing
+polygon = Polygon([[0, 0], [0, 0]], facecolor='y')
+update_polygon(-1)
+ax.add_patch(polygon)
+fig.canvas.mpl_connect('motion_notify_event', on_mouse_move)
+plt.show()
+As a bonus, did you like that fox in the banner? That was created (and well documented) by Emily Foster!
import numpy as np
+import matplotlib.pyplot as plt
+
+plt.axis('off')
+
+#head
+xhead = np.arange(-50,50,0.1)
+yhead = -0.007*(xhead*xhead) + 100
+
+plt.plot(xhead, yhead, 'darkorange')
+
+#outer ears
+xearL = np.arange(-45.8,-9,0.1)
+yearL = -0.08*(xearL*xearL) -4*xearL + 70
+
+xearR = np.arange(9,45.8,0.1)
+yearR = -0.08*(xearR*xearR) + 4*xearR + 70
+
+plt.plot(xearL, yearL, 'black')
+plt.plot(xearR, yearR, 'black')
+
+#inner ears
+xinL = np.arange(-41.1,-13.7,0.1)
+yinL = -0.08*(xinL*xinL) -4*xinL + 59
+
+xinR = np.arange(13.7,41.1,0.1)
+yinR = -0.08*(xinR*xinR) + 4*xinR + 59
+
+plt.plot(xinL, yinL, 'salmon')
+plt.plot(xinR, yinR, 'salmon')
+
+# bottom of face
+xfaceL = np.arange(-49.6,-14,0.1)
+xfaceR = np.arange(14,49.3,0.1)
+xfaceM = np.arange(-14,14,0.1)
+
+plt.plot(xfaceL, abs(xfaceL), 'darkorange')
+plt.plot(xfaceR, abs(xfaceR), 'darkorange')
+plt.plot(xfaceM, abs(xfaceM), 'black')
+
+#nose
+xnose = np.arange(-14,14,0.1)
+ynose = -0.03*(xnose*xnose) + 20
+
+plt.plot(xnose, ynose, 'black')
+
+#whiskers
+xwhiskR = [50, 70, 55, 70, 55, 70, 49.3]
+xwhiskL = [-50, -70, -55, -70, -55, -70, -49.3]
+ywhisk = [82.6, 85, 70, 65, 60, 45, 49.3]
+
+plt.plot(xwhiskR, ywhisk, 'darkorange')
+plt.plot(xwhiskL, ywhisk, 'darkorange')
+
+#eyes
+plt.plot(20,60, color = 'black', marker = 'o', markersize = 15)
+plt.plot(-20,60,color = 'black', marker = 'o', markersize = 15)
+
+plt.plot(22,62, color = 'white', marker = 'o', markersize = 6)
+plt.plot(-18,62,color = 'white', marker = 'o', markersize = 6)
+We look forward to seeing these students continue in their plotting and scientific adventures!
Posted +
Postdocs are the workers of academia. +They are the main players beyond the majority of scientific papers published in +journals and conferences. Yet, their effort is often not recognized in terms of +salary and benefits.
A few years ago, the NIH has established stipend levels for undergraduate, +predoctoral and postdoctoral trainees and fellows, the so-called NIH guidelines. +Many universities and research institutes currently adopt these guidelines for +deciding how much to pay postdocs.
One of the key problem of the NIH guidelines is that they are established at a +national level. This means that a postdoc in Buffalo is paid the same than a postdoc in Boston, +despite Buffalo is one of the most affordable city to live in the USA, +while Boston is one of the most expensive. +Every year, the NIH releases new guidelines, where the stipends are slightly +increased. Do these adjustments help a postdoc in the Boston area +take home a bit more money?
I have used Matplotlib to plot the NIH stipend levels
+(y axis) for each year of postdoctoral experience (x axis) for the past 4 years
+of NIH guidelines (color). I have also looked at the inflation of years 2017–2019
+and increased the salaries of the previous year by that percentage (dashed lines).
+
The data revealed that the salaries of 2017 were just increased by the +inflation rate for the most senior postdocs, while junior postdocs (up to 1 year +of experience) received an increase more than 2.5 times of the inflation. In +2018, all salaries were just adjusted to the inflation. In 2019, the increase was +slightly higher than the inflation level. So, overall, every year the NIH makes +sure that the postdoc salaries are, at least, adjusted to the inflation. Great!
As mentioned earlier, there are cities in the US that are more expensive than
+others, for example Boston. To partially account for such differences when
+looking at the postdoc salaries, I subtracted from each salary the average rent
+for a one-bedroom apartment in Boston.
+Of course, it also increases every year, but, unfortunately for postdocs, rent
+increases way more than the inflation. The results are below.
+
It turns out that the best year for postdocs with at least one year of experience +was actually 2016. In the subsequent years, the real estate has eaten larger and +larger portions of the postdoc salary, resulting in 2019-paid postdocs taking home +20% less money than 2016-paid postdocs with the same experience.
In the end, life is financially harder and harder for postdocs in the Boston area. +These data should be taken into account by research institutes and universities, +which have the freedom of topping up postdocs’ salaries to reflect the real cost +of living of different cities.
You can download the Jupyter notebook [here](Postdoc salary Analysis.ipynb).
Posted +
I have been creating common visualisations like scatter plots, bar charts, beeswarms etc. for a while and thought about doing something different. Since I'm an avid football fan, I thought of ideas to represent players’ usage or involvement over a period (a season, a couple of seasons). I have seen some cool visualisations like donuts which depict usage and I wanted to make something different and simple to understand. I thought about representing batteries as a form of player usage and it made a lot of sense.
For players who have been barely used (played fewer minutes) show a large amount of battery present since they have enough energy left in the tank. And for heavily used players, do the opposite i.e. show drained or less amount of battery
So, what is the purpose of a battery chart? You can use it to show usage, consumption, involvement, fatigue etc. (anything usage related).
The image below is a sample view of how a battery would look in our figure, although a single battery isn't exactly what we are going to recreate in this tutorial.
Before jumping on to the tutorial, I would like to make it known that the function can be tweaked to fit accordingly depending on the number of subplots or any other size parameter. Coming to the figure we are going to plot, there are a series of steps that is to be considered which we will follow one by one. The following are those steps:-
What is our use case?
The first and foremost part is to import the essential libraries so that we can leverage the functions within. In this case, we will import the libraries we need.
import pandas as pd
+import matplotlib.pyplot as plt
+from matplotlib.path import Path
+from matplotlib.patches import FancyBboxPatch, PathPatch, Wedge
+The functions imported from matplotlib.path and matplotlib.patches will be used to draw lines, rectangles, boxes and so on to display the battery as it is.
The next part is to define a function named draw_battery(), which will be used to draw the battery. Later on, we will call this function by specifying certain parameters to build the figure as we require. The following below is the code to build the battery -
def draw_battery(fig, ax, percentage=0, bat_ec="grey",
+ tip_fc="none", tip_ec="grey",
+ bol_fc="#fdfdfd", bol_ec="grey", invert_perc=False):
+ '''
+ Parameters
+ ----------
+ fig : figure
+ The figure object for the plot
+ ax : axes
+ The axes/axis variable of the figure.
+ percentage : int, optional
+ This is the battery percentage - size of the fill. The default is 0.
+ bat_ec : str, optional
+ The edge color of the battery/cell. The default is "grey".
+ tip_fc : str, optional
+ The fill/face color of the tip of battery. The default is "none".
+ tip_ec : str, optional
+ The edge color of the tip of battery. The default is "grey".
+ bol_fc : str, optional
+ The fill/face color of the lighning bolt. The default is "#fdfdfd".
+ bol_ec : str, optional
+ The edge color of the lighning bolt. The default is "grey".
+ invert_perc : bool, optional
+ A flag to invert the percentage shown inside the battery. The default is False
+
+ Returns
+ -------
+ None.
+
+ '''
+ try:
+ fig.set_size_inches((15,15))
+ ax.set(xlim=(0, 20), ylim=(0, 5))
+ ax.axis("off")
+ if invert_perc == True:
+ percentage = 100 - percentage
+ # color options - #fc3d2e red & #53d069 green & #f5c54e yellow
+ bat_fc = "#fc3d2e" if percentage <= 20 else "#53d069" if percentage >= 80 else "#f5c54e"
+
+ '''
+ Static battery and tip of battery
+ '''
+ battery = FancyBboxPatch((5, 2.1), 10, 0.8,
+ "round, pad=0.2, rounding_size=0.5",
+ fc="none", ec=bat_ec, fill=True,
+ ls="-", lw=1.5)
+ tip = Wedge((15.35, 2.5), 0.2, 270, 90, fc="none",
+ ec=bat_ec, fill=True,
+ ls="-", lw=3)
+ ax.add_artist(battery)
+ ax.add_artist(tip)
+
+ '''
+ Filling the battery cell with the data
+ '''
+ filler = FancyBboxPatch((5.1, 2.13), (percentage/10)-0.2, 0.74,
+ "round, pad=0.2, rounding_size=0.5",
+ fc=bat_fc, ec=bat_fc, fill=True,
+ ls="-", lw=0)
+ ax.add_artist(filler)
+
+ '''
+ Adding a lightning bolt in the centre of the cell
+ '''
+ verts = [
+ (10.5, 3.1), #top
+ (8.5, 2.4), #left
+ (9.5, 2.4), #left mid
+ (9, 1.9), #bottom
+ (11, 2.6), #right
+ (10, 2.6), #right mid
+ (10.5, 3.1), #top
+ ]
+
+ codes = [
+ Path.MOVETO,
+ Path.LINETO,
+ Path.LINETO,
+ Path.LINETO,
+ Path.LINETO,
+ Path.LINETO,
+ Path.CLOSEPOLY,
+ ]
+ path = Path(verts, codes)
+ bolt = PathPatch(path, fc=bol_fc,
+ ec=bol_ec, lw=1.5)
+ ax.add_artist(bolt)
+ except Exception as e:
+ import traceback
+ print("EXCEPTION FOUND!!! SAFELY EXITING!!! Find the details below:")
+ traceback.print_exc()
+
+Once we have created the API or function, we can now implement the same. And for that, we need to feed in required data. In our example, we have a dataset that has the list of Liverpool players and the minutes they have played in the past two seasons. The data was collected from Football Reference aka FBRef.
We use the read excel function in the pandas library to read our dataset that is stored as an excel file.
data = pd.read_excel("Liverpool Minutes Played.xlsx")
+Now, let us have a look at how the data looks by listing out the first five rows of our dataset -
data.head()
+
Now that everything is ready, we go ahead and plot the data. We have 25 players in our dataset, so a 5 x 5 figure is the one to go for. We'll also add some headers and set the colors accordingly.
fig, ax = plt.subplots(5, 5, figsize=(5, 5))
+facecolor = "#00001a"
+fig.set_facecolor(facecolor)
+fig.text(0.35, 0.95, "Liverpool: Player Usage/Involvement", color="white", size=18, fontname="Libre Baskerville", fontweight="bold")
+fig.text(0.25, 0.92, "Data from 19/20 and 20/21 | Battery percentage indicate usage | less battery = played more/ more involved", color="white", size=12, fontname="Libre Baskerville")
+We have now now filled in appropriate headers, figure size etc. The next step is to plot all the axes i.e. batteries for each and every player. p is the variable used to iterate through the dataframe and fetch each players data. The draw_battery() function call will obviously plot the battery. We also add the required labels along with that - player name and usage rate/percentage in this case.
p = 0 #The variable that'll iterate through each row of the dataframe (for every player)
+for i in range(0, 5):
+ for j in range(0, 5):
+ ax[i, j].text(10, 4, str(data.iloc[p, 0]), color="white", size=14, fontname="Lora", va='center', ha='center')
+ ax[i, j].set_facecolor(facecolor)
+ draw_battery(fig, ax[i, j], round(data.iloc[p, 8]), invert_perc=True)
+ '''
+ Add the battery percentage as text if a label is required
+ '''
+ ax[i, j].text(5, 0.9, "Usage - "+ str(int(100 - round(data.iloc[p, 8]))) + "%", fontsize=12, color="white")
+ p += 1
+Now that everything is almost done, we do some final touchup and this is a completely optional part anyway. Since the visualisation is focused on Liverpool players, I add Liverpool's logo and also add my watermark. Also, crediting the data source/provider is more of an ethical habit, so we go ahead and do that as well before displaying the plot.
liv = Image.open('Liverpool.png', 'r')
+liv = liv.resize((80, 80))
+liv = np.array(liv).astype(np.float) / 255
+fig.figimage(liv, 30, 890)
+fig.text(0.11, 0.08, "viz: Rithwik Rajendran/@rithwikrajendra", color="lightgrey", size=14, fontname="Lora")
+fig.text(0.8, 0.08, "data: FBRef/Statsbomb", color="lightgrey", size=14, fontname="Lora")
+plt.show()
+So, we have the plot below. You can customise the design as you want in the draw_battery() function - change size, colours, shapes etc
Posted +
Earth's temperatures are rising and nothing shows this in a simpler, +more approachable graphic than the “Warming Stripes”. +Introduced by Prof. Ed Hawkins they show the temperatures either for +the global average or for your region as colored bars from blue to red for the last 170 years, available at #ShowYourStripes.
The stripes have since become the logo of the Scientists for Future. +Here is how you can recreate this yourself using Matplotlib.
We are going to use the HadCRUT4 dataset, published by the Met Office. +It uses combined sea and land surface temperatures. +The dataset used for the warming stripes is the annual global average.
First, let's import everything we are going to use. +The plot will consist of a bar for each year, colored using a custom +color map.
import matplotlib.pyplot as plt
+from matplotlib.patches import Rectangle
+from matplotlib.collections import PatchCollection
+from matplotlib.colors import ListedColormap
+import pandas as pd
+Then we define our time limits, our reference period for +the neutral color and the range around it for maximum saturation.
FIRST = 1850
+LAST = 2018 # inclusive
+
+# Reference period for the center of the color scale
+FIRST_REFERENCE = 1971
+LAST_REFERENCE = 2000
+LIM = 0.7 # degrees
+Here we use pandas to read the fixed width text file, only the +first two columns, which are the year and the deviation from the +mean from 1961 to 1990.
# data from
+# https://www.metoffice.gov.uk/hadobs/hadcrut4/data/current/time_series/HadCRUT.4.6.0.0.annual_ns_avg.txt
+df = pd.read_fwf(
+ 'HadCRUT.4.6.0.0.annual_ns_avg.txt',
+ index_col=0,
+ usecols=(0, 1),
+ names=['year', 'anomaly'],
+ header=None,
+)
+
+anomaly = df.loc[FIRST:LAST, 'anomaly'].dropna()
+reference = anomaly.loc[FIRST_REFERENCE:LAST_REFERENCE].mean()
+This is our custom colormap, we could also use one of
+the colormaps that come with matplotlib, e.g. coolwarm or RdBu.
# the colors in this colormap come from http://colorbrewer2.org
+# the 8 more saturated colors from the 9 blues / 9 reds
+cmap = ListedColormap([
+ '#08306b', '#08519c', '#2171b5', '#4292c6',
+ '#6baed6', '#9ecae1', '#c6dbef', '#deebf7',
+ '#fee0d2', '#fcbba1', '#fc9272', '#fb6a4a',
+ '#ef3b2c', '#cb181d', '#a50f15', '#67000d',
+])
+We create a figure with a single axes object that fills the full area +of the figure and does not have any axis ticks or labels.
fig = plt.figure(figsize=(10, 1))
+
+ax = fig.add_axes([0, 0, 1, 1])
+ax.set_axis_off()
+Finally, we create bars for each year, assign the +data, colormap and color limits and add it to the axes.
# create a collection with a rectangle for each year
+col = PatchCollection([
+ Rectangle((y, 0), 1, 1)
+ for y in range(FIRST, LAST + 1)
+])
+
+# set data, colormap and color limits
+col.set_array(anomaly)
+col.set_cmap(cmap)
+col.set_clim(reference - LIM, reference + LIM)
+ax.add_collection(col)
+Make sure the axes limits are correct and save the figure.
ax.set_ylim(0, 1)
+ax.set_xlim(FIRST, LAST + 1)
+
+fig.savefig('warming-stripes.png')
+
hugo says hello!
- - -:wq - -$ -``` - -Build the web site and then verify the results. - -``` -$ hugo --verbose -INFO: 2014/09/29 Using config file: /Users/quoha/Sites/zafta/config.toml -INFO: 2014/09/29 syncing from /Users/quoha/Sites/zafta/themes/zafta/static/ to /Users/quoha/Sites/zafta/public/ -INFO: 2014/09/29 syncing from /Users/quoha/Sites/zafta/static/ to /Users/quoha/Sites/zafta/public/ -WARN: 2014/09/29 Unable to locate layout: [404.html theme/404.html] -0 draft content -0 future content -0 pages created -0 tags created -0 categories created -in 2 ms - -$ find public -type f -name '*.html' | xargs ls -l --rw-r--r-- 1 quoha staff 78 Sep 29 21:26 public/index.html - -$ cat public/index.html - - - -hugo says hello!
- -``` - -#### Live Reload - -Note: If you're running the server with the `--watch` option, you'll see different content in the file: - -``` -$ cat public/index.html - - - -hugo says hello!
- - -``` - -When you use `--watch`, the Live Reload script is added by Hugo. Look for live reload in the documentation to see what it does and how to disable it. - -### Build a "Dynamic" Home Page - -"Dynamic home page?" Hugo's a static web site generator, so this seems an odd thing to say. I mean let's have the home page automatically reflect the content in the site every time Hugo builds it. We'll use iteration in the template to do that. - -#### Create New Posts - -Now that we have the home page generating static content, let's add some content to the site. We'll display these posts as a list on the home page and on their own page, too. - -Hugo has a command to generate a skeleton post, just like it does for sites and themes. - -``` -$ hugo --verbose new post/first.md -INFO: 2014/09/29 Using config file: /Users/quoha/Sites/zafta/config.toml -INFO: 2014/09/29 attempting to create post/first.md of post -INFO: 2014/09/29 curpath: /Users/quoha/Sites/zafta/themes/zafta/archetypes/default.md -ERROR: 2014/09/29 Unable to Castmy first post
- - - - -$ cat public/post/second/index.html - - - -my second post
- - - -$ -``` - -Notice that the posts now have content. You can go to localhost:1313/post/first to verify. - -### Linking to Content - -The posts are on the home page. Let's add a link from there to the post. Since this is the home page, we'll update its template. - -``` -$ vi themes/zafta/layouts/index.html - - - - {{ range first 10 .Data.Pages }} -